13

I conjecture the following inequality:

For $x > 1$, and $n$ a positive integer, $$\sum_{k=1}^{n}\{kx\}\le\dfrac{n}{2}x.$$

For $n=1$, the inequality becomes $$\{x\}\le\dfrac{x}{2}\Longleftrightarrow \{x\}\le [x];$$ and, for $n = 2$, it becomes $$\{x\}+\{2x\}\le x\Longleftrightarrow \{2x\}\le [x],$$ which is obvious since $[x]\ge 1>\{2x\}$.

If $x\ge 2$, the inequality is obvious, since $$\dfrac{n}{2}x\ge n\ge\sum_{k=1}^{n}\{kx\}.$$ However, I cannot prove it for $1 < x < 2$.

LSpice
  • 11,423
math110
  • 4,230
  • I found this question very hard to read, so have edited to try to clarify. Obviously, please feel free to revert or improve the edit. – LSpice Nov 10 '18 at 02:33
  • 5
    Isn't MSE a right forum for such questions? – user64494 Nov 10 '18 at 03:41
  • 2
    I suppose that ${x}$ means fractional part and $[x]$ means integer part? – Nate Eldredge Nov 10 '18 at 04:47
  • @NateEldredge,yes, – math110 Nov 10 '18 at 04:47
  • 13
    Look at the integer grid squares the line through the origin with slope $x$ visits: you get $n$ right triangles with heights ${kx}$ and bases $\leqslant1$. – მამუკა ჯიბლაძე Nov 10 '18 at 05:09
  • 1
    @user64494 looks of MO level, as for me – Fedor Petrov Nov 10 '18 at 12:20
  • @Fedor Petrov: Which are the applications of the inequality or/and the methods of its proof? – user64494 Nov 10 '18 at 13:56
  • 3
    I do not know the methods of its proof (I do not know the proof, and even am not sure that it is true), but the estimates of the remainder in the approximate formulae for the number of lattice points in certain regions (this specific question is about triangle with vertices $(0,0),(n,0),(n,xn)) attract a lot of interest. Aswell as the sums of periodic functions along arithmetic progressions. – Fedor Petrov Nov 10 '18 at 14:14
  • 2
    This is a reasonable MO question. There are ways to estimate $\sum_{k=1}^n \left({kx}-\frac12\right)$ that involve expanding using Fourier series. The quantity$T-\frac12$ is the first Bernoulli polynoimal, which is a little trickier to handle than using $B_d$ for $d\ge2$, due to conditional convergence issues. My recollection is that one gets an extra $\log(n)$, but I don't have time to track it down right now. It may be in the following paper: P. E. Blanksby and H. L. Montgomery, Algebraic integers near the unit circle, Acta Arith. XVIII (1971), 355–369 – Joe Silverman Nov 10 '18 at 14:22
  • @Joe Silverman: What do you denote by $T$?$B_d$? – user64494 Nov 10 '18 at 14:44
  • $T$ is just a variable. $B_d(T)$ is the $d$'th Bernoulli polynomial. There are upper bounds for sums of this sort, although usually one weights by the Fejar kernel, so one looks at sums of the form $$\sum_{k=1}^n \left(1-\frac{k}{n+1}\right)B_d\left(\left{\frac{kx}{n}\right}\right).$$ Since $B_1(T)=T-\frac12$,this is closely related to your sum. The expansion of $B_d({t})$ is some constant multiple of $\sum_{m\ne0} e^{2\pi i mt}/m^d$ (or something like that). – Joe Silverman Nov 10 '18 at 15:43
  • 4
    From this paper I conclude that $\sum_{k=1}^n{kx}$ grows as $n/2+c\log n$ (the coefficient $c=1/256$), which is consistent with your upper bound of $nx/2$ for $x>1$. – Carlo Beenakker Nov 10 '18 at 18:28

3 Answers3

28

As მამუკა ჯიბლაძე said, the proof is a picture though I had trouble reconstructing the picture of his and came up with a slightly different one.

Let $0<y<1$. Consider the rectangles with bases $[k-1,k]$ of heights $[ky]$ for $k=1,2,\dots,n$. They cover the triangle with the vertices $(0,0),(n,0),(n,ny)$ up to several triangles of height $\le 1$ with sum of bases $\le n$. This proves the inequality $$ \sum_{k=1}^n[ky]\ge \frac{n^2y}2-\frac n2\,. $$ Now, for $x=1+y\in(1,2)$, we have $$ \sum_{k=1}^n\{kx\}=\sum_{k=1}^n\{ky\}=\sum_{k=1}^n ky-\sum_{k=1}^n[ky] \\ \le \frac{n(n+1)y}2-\frac{n^2y}2+\frac n2=\frac n2(1+y)=\frac n2x\,. $$

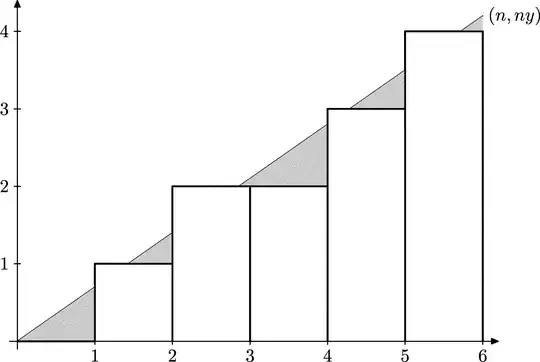
picture for n=6 and y=0.7

Martin Sleziak
  • 4,608
fedja
  • 59,730
  • Sorry I don't get the argument. You want the large triangle to contain the rectangles plus some small triangles whose areas sum up to $n/2$. What are your small triangles? – abx Nov 11 '18 at 08:58
  • @abx. No, the large triangle does not contain the rectangles. They stick out a bit in places. The small triangles are what is in the large triangle but not in the rectangles. Have you tried to draw a picture? If you draw it, you'll see them immediately. – fedja Nov 11 '18 at 13:35
  • Ah, OK. I did draw a picture, but with the base of the rectangle with height $[ky]$ being wrongly $[k,k+1]$. Thanks! – abx Nov 11 '18 at 13:45
  • @fedja,can you draw a picture to help understand?I can't understand your first mean – math110 Nov 16 '18 at 11:15
  • @Martin Sleziak: Nice picture, but it would be even nicer to draw the line segments joining the vertices at $x=1,2,4,5$, i.e. the convex hull of the figure — the point is that it is above the line of slope $y$. Comparing the areas gives the required inequality. – abx Nov 16 '18 at 20:26
  • @abx You can check whether this picture is approximately what you had in mind: https://i.stack.imgur.com/0UyOS.png In any case, if there should be further discussion specifically about the picture we could continue in chat - so that we do not leave too many irrelevant comments here. (I will leave also metapost source there, in case somebody wants to improve the picture further.) – Martin Sleziak Nov 16 '18 at 20:58
  • @Martin Sleziak: Yes, this is exactly what I was suggesting. Thanks! – abx Nov 16 '18 at 21:01
  • This shows that the inequality is closest to sharp when the triangles have height almost $1$ and cover the space almost entirely, which happens when $y=1/k-\epsilon$ so $x=1+1/k-\epsilon$. – Will Sawin Nov 18 '18 at 01:57
  • 2
    "the picture of his": did you look up the name to determine that this user is male? Or is this an instance of the implicit gender biases we all carry, where we simply assume that people discussing mathematics are male? It's worth paying attention to such things, because implicit bias in mathematics really harms women who want to participate. – Greg Martin Nov 18 '18 at 06:48
  • @GregMartin No, I didn't. I don't know the language the name is written in (do you?). The "implicit bias" is just the common default English construct. If you have a valid reason to suspect that the user in question is female, I'll be happy to change the pronoun. – fedja Nov 18 '18 at 12:28
  • @GregMartin I will just add to the previous comment that in this specific case both the photo in the user's profile and the user's website found after searching for this specific name suggest that this is indeed a masculine given name. (Although I understand that when in doubt it is better to use gender neutral language.) – Martin Sleziak Nov 18 '18 at 15:48
  • 1
    @MartinSleziak (and others). 5 seconds after I clicked on the CV on that website I've got the "Microsoft critical alert" scam message. May be a pure coincidence, of course, but I'd rather report it here :-) – fedja Nov 18 '18 at 16:58
  • @fedja I'll just mention that I forwarded the information about the problems with the website to this user: https://chat.stackexchange.com/transcript/19138/2018/11/19 (I'd guess that several of these comments are completely unrelated to the post, and they might be eventually cleaned up. But since we already went into this topic, it was probably worth mentioning.) – Martin Sleziak Nov 20 '18 at 14:02
9

Here is a different, more algebraic proof. I don't know if there is any reason to prefer it to the visual proof.

It is sufficient to prove the inequality if we take $\{x\}$ to round up instead of down, as that is a stronger inequality.

If we raise $x$ by $\epsilon$, where $\epsilon$ is small enough that no fractional part wraps around, the left side increases by $n (n+1) \epsilon/2$ and the right side by $n \epsilon/2$. We can do this unless $xk$ is an integer for some $1 \leq k \leq n$. Because the increase on the left is greater than the increase on the right, we can reduce to the case where $xk$ is an integer for some $1 \leq k \leq n$, say $x=a/b$ with $1 \leq b \leq n$ and $a,b$ relatively prime. We have

$$ \sum_{k=1}^n \left\{ k \frac{a}{b} \right\} = \sum_{k=1}^b \left\{ k \frac{a}{b} \right\} +\sum_{k=b+1}^n \left\{ k \frac{a}{b} \right\} $$

For the first term, we use the fact that $a$ is a permutation of residue classes mod $b$, so

$$ \sum_{k=1}^b \left\{ k \frac{a}{b} \right\} = \sum_{k=1}^b \left\{ \frac{k}{b} \right\}= \sum_{k=1}^b \frac{k}{b} = \frac{b (b+1)}{2b} \leq \frac{b a}{2b} = \frac{bx}{2} $$

For the second term, we use periodicity and induction on $n$, so

$$\sum_{k=b+1}^n \left\{ k \frac{a}{b} \right\} = \sum_{k=1}^{n-b} \left\{ k \frac{a}{b} \right\} \leq \frac{ (n-b) x}{2} $$

Summing, we get an upper bound of $\frac{nx}{2}$, as desired (and as necessary for the induction step).

Will Sawin
  • 135,926
7

This is a proof smilar to Will Sawin's but with no induction.

Set $y=x-1$. We need to prove that the average of $\{y\},\dots,\{ny\}$ is at most $x/2$. The numbers $y,2y,\dots,ny$ split into contiguous groups, each group with the same integer part. It suffices to show that the average of the fractional parts for each group is at most $x/2$. Those fractional parts form an arithmetical sequence, so their average is half the sum of the first and the last term. As the fractional part of the first term in the group is at most $y$, this average is bounded by $\frac{y+1}2=x/2$, as desired.

Ilya Bogdanov
  • 22,168