Unfortunately, due to my ignorance, my present knowledge is limited to the cobordism Theory of Differentiable Manifolds.
- Cobordism Theory for DIFF/Differentiable/smooth manifolds
However, there are Topological Manifolds which are not Differentiable Manifolds.
So my question here for experts is that what do I need to beware and pay attention in order to master a cobordism theory of Topological Manifolds? What are the main differences of the computations of the bordism groups for the given following structures:
Say,
Cobordism Theory of TOP/topological manifolds
Cobordism Theory for PDIFF/piecewise differentiable manifolds
Cobordism Theory for PL/piecewise-linear manifolds
p.s. Are there Spin, Pin$^+$, and Pin$^-$ versions of these cobordism theories of Topological Manifolds computed in the literature explicitly?
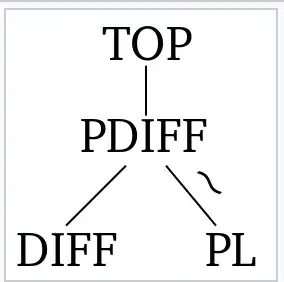
bit.lylink in a comment above points to a diagram ontikzcd.yichuanshen.de. (Just in case the link breaks.) – The Amplitwist Sep 05 '22 at 12:52