Napkin Folding Problem / Rumpled Ruble Problem

Question

I am an outsider to this group. I'm a journalist and am working on a piece about theoretical math/geometry. Simply put, when a napkin is folder in such a way to increase its perimeter is that strictly theoretical? Like, the physical limitations of the world (tension and width of cloth) make it impossible to increase the perimeter.

Can someone help me understand what is really being discussed when geometry people discuss the folding of a ruble or napkin?

-thanks

It might be better to post this on mathematics.stackexchange. Mathematicians often use ideal models to tackle problems. In this case, "infinitely thin" paper that does not stretch is a good model for the napkin folding problem. If there is a solution with only finitely many folds, then one can try a slightly different model where the paper behaves more like "ruble paper", to see if the solution can be adapted. Gerhard "Wants Lots Of Dollar Models" Paseman, 2019.09.11. — Gerhard Paseman, Sep 11 '19 at 16:17
You might consult "Is the “Napkin conjecture” open? (origami)." In particular, this folding could be executed by hand. — Joseph O'Rourke, Sep 11 '19 at 16:30

Carlo Beenakker · Answer 1 · 2019-09-11T16:43:09.823

I think you will find this discussion of the napkin folding problem instructive: Chapter 5 of Lectures on piecewise distance preserving maps. The problem involves "Origami moves", meaning folding and unfolding of a thin sheet of paper, and asking whether the perimeter of the flattened folded sheet can increase.

The answer is no if all layers of the folded sheet are always folded simultaneously, as in this figure:

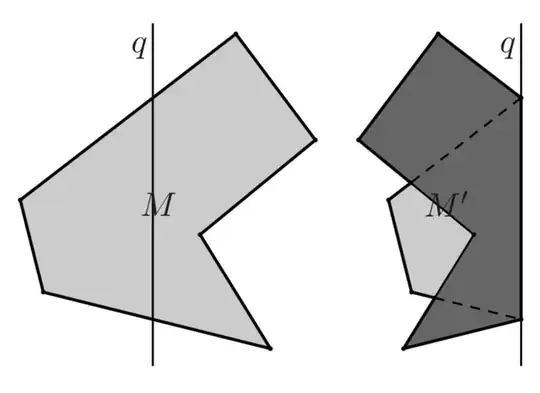
You have to allow for unfolding of a folded layer, as in the figure below, which actually does increase the perimeter, however, not yet beyond the perimeter of the original square.

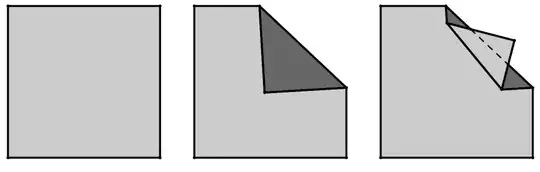
18th century origami masters already discovered, before this problem was posed by mathematicians in the 20th century, that you can in fact increase the final perimeter beyond the initial perimeter, for example in this crane figure:

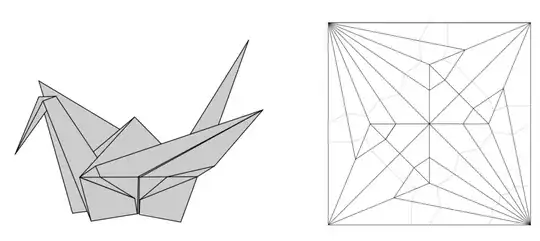
The perimeter of the flattened crane is about 0.5% larger than the perimeter of the initial square. The crane has 80 layers of folded paper. By increasing the number of folds it is possible to make the final perimeter as large as one wants, without mathematical limit. There is of course a physical limit, due to the nonzero thickness of the paper.

thank you very much, this was helpful. – user145712 Sep 12 '19 at 17:27 — user145712, Sep 12 '19 at 17:27

Napkin Folding Problem / Rumpled Ruble Problem

1 Answers1