Nice proof of inequality $(1-x^p)^{1/p}(1-x^q)^{1/q}\ge (1-x)(1+x^c)^{1/c}$ where $2^{1/c} = p^{1/p} q^{1/q}$?

Question

Let $0\leq x < 1$, $1 \leq p < \infty$ and $q$ be the conjugate exponent defined by $$1/p + 1/q = 1.$$

I am looking for a nice proof that

$$ \frac{(1-x^p)^{1/p}(1-x^q)^{1/q}}{(1-x)(1+x^c)^{1/c}} \geq 1,$$ where $c$ is defined via $$2^{1/c} = p^{1/p} q^{1/q}.$$

The number $c$ is defined so that the inequality holds as we take a limit as $x \to 1$. I checked it for various values of $p$ graphically and it seems to be true. It holds with equality in the case $p=q=2$.

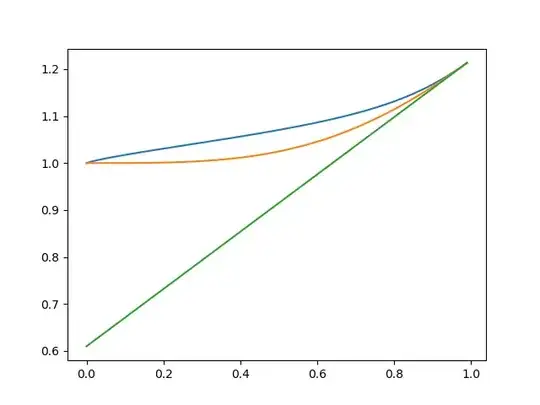
Edit: Here is a graph, for $p=20$.

The blue line is the graph of $$f(x) = \frac{(1-x^p)^{1/p} (1-x^q)^{1/q}}{1-x}.$$ The orange line is $(1+x^c)^{1/c}$, as in the original question. The green line is $2^{1/c - 1}(1+x)$ which was proved to be a lower bound for $f$ by Willie Wong in the comments.

It may be worth noting that if we replace the denominator by $2^{1/c - 1} (1-x)(1+x)$ (which is $\leq (1-x)(1 + x^c)^{1/c}$ so doesn't imply the desired the inequality), the inequality would be immediately be implied by Holder's inequality on the integral $\int_x^1 s^2~ ds/s$. So you are looking for something sharper that captures a bit of the error of naive applications of Holder. — Willie Wong, Oct 07 '19 at 15:41
It seems interesting enough for MO. In the past, I got stuck in similar inequalities which were valuable to our research; e.g. see this post https://mathoverflow.net/questions/246919/mixing-convex-and-concave-for-convexity — T. Amdeberhan, Oct 07 '19 at 18:58
@T. Amdeberhan I see "a curious inequality" in the link. Is not that art for art's sake too? — user64494, Oct 07 '19 at 19:10
@user64494, the "curious inequality" in the link is directly related to a problem arising in potential theory about whether animals should gather close to each other in order to decrease the total rate of heat loss. See https://mathoverflow.net/questions/217530/a-problem-of-potential-theory-arising-in-biology/230065#230065 — Paata Ivanishvili, Oct 07 '19 at 21:00
@Paata Ivanishvili Sorry, I don't see any relation. Can you kindly elaborate your comment? TIA. — user64494, Oct 08 '19 at 05:45
If one takes two balls of equal radii at distance d, and a harmonic function $u$ in 3D such that its value is 1 on the boundaries of the balls, 0 at infinity, and it is defined in the complement of the union of balls then the quantity $d \mapsto 2\int_{\partial B} \frac{\partial u}{\partial n} ds$ represents the "total rate of loss of heat", and it equals to $(d-d^{-1}) \sum_{k=0}^{\infty}\frac{1}{d^{2k+1}+1}$ up to some universal multiplicative constants (and shifting in variable $d$). The question I asked in the link is whether the latter is increasing function. — Paata Ivanishvili, Oct 08 '19 at 05:53
@Paata Ivanishvili Sorry, I still don't see any relation with the question under consideration. — user64494, Oct 08 '19 at 11:26
A 3-D plot makes clear that the inequality is true. Also, it never gets very large. There are two equivalent maxima of value 1.049502 at $p$=1.096610, $q$=11.350912, $x$=0.332307 and the same with $p$ and $q$ swapped. — Brendan McKay, Oct 08 '19 at 13:00
@Lucia Thank you for your question. In my (and not only my) opinion, art for art's sake is useless. — user64494, Oct 08 '19 at 15:36
@user64494 Then why spend time on this site decrying it? If other mathematicians find it interesting or useful, who are you to declare that it is not appropriate for this site? — Yemon Choi, Oct 11 '19 at 02:19
@George Shakan You are looking for a nice proof (e.g., you have an ugly proof), or any proofs even not nice (ugly or complicated)? — River Li, Oct 21 '19 at 16:24
@George Shakan I came up with a possible proof which is not nice. We may wait for nice proofs. (Corrected the typo of the comment.) — River Li, Oct 27 '19 at 07:06

Nice proof of inequality $(1-x^p)^{1/p}(1-x^q)^{1/q}\ge (1-x)(1+x^c)^{1/c}$ where $2^{1/c} = p^{1/p} q^{1/q}$?

0 Answers0