Lattices on classical combinatorial families

Question

I am asking for examples of lattices defined on classical combinatorial families, such as Permutations, Catalan objects, set partitions or integer partitions, graphs.

I am mosty interested in lattices defined on the objects of a fixed size.

To make later usage easier, I would like to combine all lattices defined on one set of objects into one answer, and identify sets of objects which are in bijection.

My motivation for creating this list is that I realized how limited my supply of examples of lattices is.

Answer 1

Lattices are prevalent when one deals with integer partitions. Let me give a few examples with pictures, that I hope you will enjoy despite the poor quality due to bitmap conversion.

The dominance order, that you already cited, is a lattice; it is not distributive and not graded, but it has nice self-similar properties. Here is a picture of its Hasse diagrams for $n=7$ and $n=20$:

                                    

   

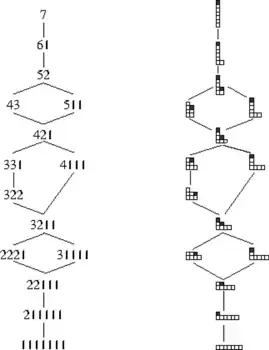
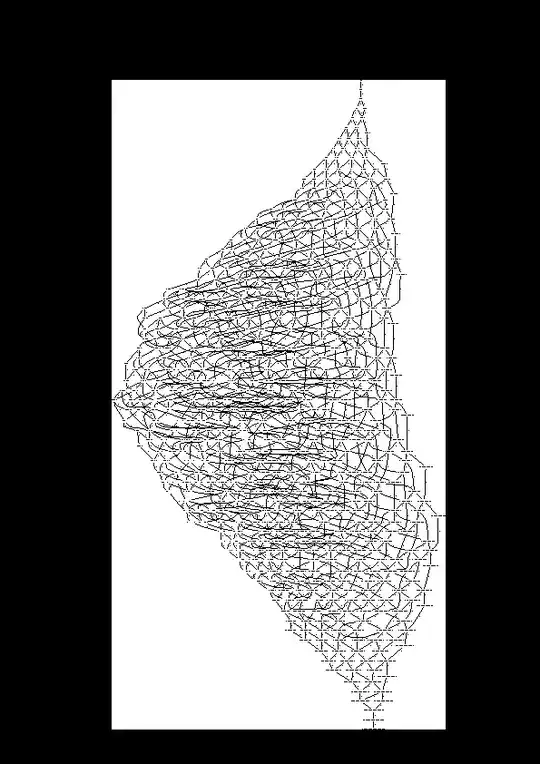
The reachable configurations of the linear Sand Pile Model (SPM), where one starts with a pile of $n$ grains, and they may fall under the condition that the sequence of piles remains decreasing, is also a lattice. It is a sub-order of the lattice above. It is not distributive either, but it is graded, and has nice self-similar features too. Here is the Hasse diagram for $n=40$.

                             

Ice Pile Models (IPM) are generalizations of the two above cases, where the grains may slip from one column to another under some conditions. The induced orders are non-graded lattices, and one may obtain not only partitions but also compositions of a given integer.

The examples above are partitions of a given integer; one may also consider integer partitions of given maximal part and/or number of parts.

This leads to finite distributive sub-lattices of the Young Lattice, strongly related to Dyck paths, already cited in previous answers. For instance, if we consider partitions in at most $3$ parts of value at most $3$, we obtain the following representations (the rightmost one is the lattice of Dyck paths with three steps in each direction):

                    

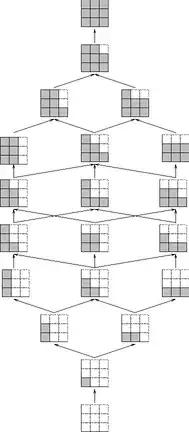
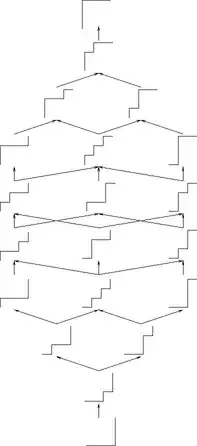
These can be generalized to plane partitions (or piles of cubes), solid partitions and actually generalized integer partitions on graphs introduced, I think, by Stanley in his seminal book "Ordered Structures and Partitions". Again, we obtain distributive lattices, and here is the case of planar partitions contained in a 3x3x2 volume:

                                       

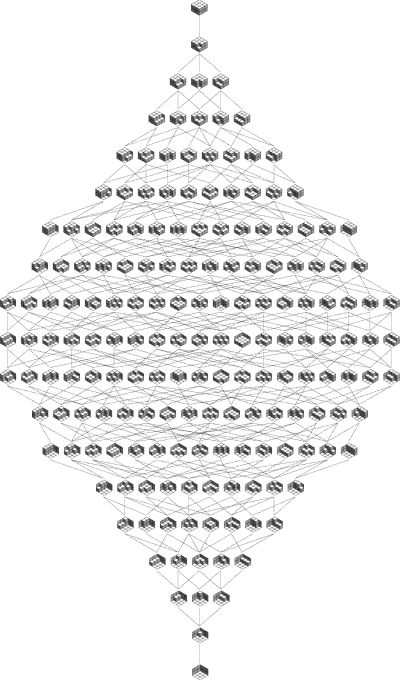
As you may see above, these partitions are equivalent to tilings of an hexagon with lozenges, with the order induced by flips of three tiles. In higher dimensions, we obtain tilings of 2D-gons, with the same flip ordering. They are not always lattices, but they are disjoint unions of distributive lattices, because of their relation to generalized integer partitions. For instance, here is the set of all tilings of a unit decagon:

                       

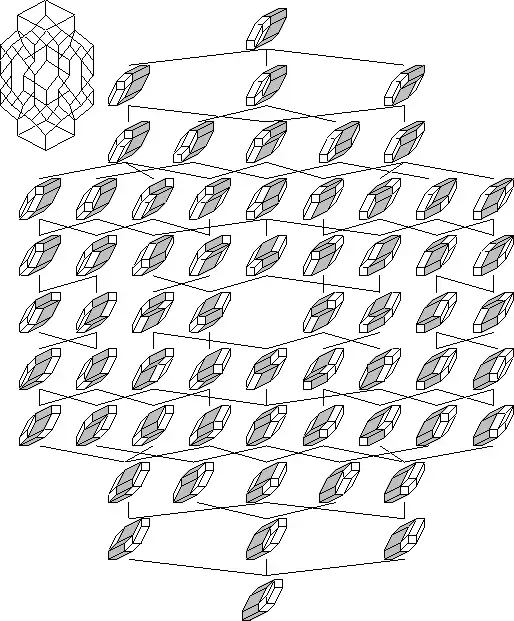
Other kinds of tilings with flips induce distributive lattices, like tilings by dominoes, and generalized tilings with height functions.

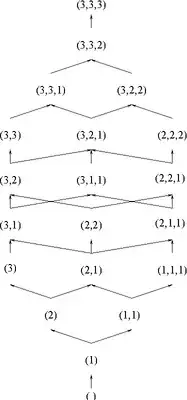
Let me add a last example, because I love its drawing. If one considers, for a given $b$, the different ways to write a given number $n$ as a sum of powers of $b$, then one obtains a self-similar distributive lattice. For instance, for $n=80$ and $b=2$:

Answer 2

Catalan objects, http://oeis.org/A000108

• noncrossing partition lattice (also known as Kreweras lattice)
• Tamari lattice - this lattice is not distributive but it is semidistributive
• Dyck paths ordered by containment (also known as Stanley lattice) - this lattice is distributive

Bernardi, Olivier; Bonichon, Nicolas, Intervals in Catalan lattices and realizers of triangulations, J. Comb. Theory, Ser. A 116, No. 1, 55-75 (2009). ZBL1161.06001.

Answer 3

Permutations, http://oeis.org/A000142

• weak (Bruhat) order - this lattice is not distributive, but it is semidistributive
• shard intersection order
• the ``bubble-sort'' order or more generally any of the sorting orders of Armstrong - this lattice (which sits between weak and strong order) is distributive

Reading, Nathan, Noncrossing partitions and the shard intersection order, Krattenthaler, Christian (ed.) et al., Proceedings of the 21st annual international conference on formal power series and algebraic combinatorics, FPSAC 2009, Hagenberg, Austria, July 20–24, 2009. Nancy: The Association. Discrete Mathematics & Theoretical Computer Science (DMTCS). Discrete Mathematics and Theoretical Computer Science. Proceedings, 745-756 (2009). ZBL1391.05283.

Answer 4

Set partitions, https://oeis.org/A000110

• refinement order

Answer 5

Alternating Sign Matrices, https://oeis.org/A005130

• distributive lattice of monotone triangles ordered componentwise, which is the MacNeille completion of (strong) Bruhat order on the symmetric group.

Answer 6

$n^{n-2}$ objects (labeled trees or parking functions)

• the Cartesian product of $n-2$ chains of length $n$ can be interpreted as a (distributive) lattice on the Prüfer codes of labeled trees on $n$ vertices.

Answer 7

Fibonacci numbers: Two examples of distributive lattice structures

$\bullet$ Dominance Order on $\Bbb{YF}_n$: A fibonacci word is a string of the form $u = a_1 \cdots a_k$ with digits $a_i \in \{1, 2\}$. Define its length by $|u| := a_1 + \cdots + a_k$ and the let $\Bbb{YF}_n$ denote the set of all fibonacci words of length $|u|=n$. Clearly the cardinality of $\Bbb{YF}_n$ is $F_n$ where $F_n$ is the $n$-th fibonacci number. Given two fibonacci words $u= a_1 \cdots a_k$ and $v = b_1 \dots b_\ell$ of equal length declare $u \unlhd v$ if $a_1 + \cdots + a_i \leq b_1 + \cdots + b_i$ for $1 \leq i \leq \mathrm{min}(k,\ell)$. This is a distributive lattice.

$\bullet$ Ideals of the Zig-Zag Poset $\mathcal{Z}_n$: The Zig-Zag poset $\mathcal{Z}_n$ is the index set $[1, \dots, n]$ where all even numbers are maximal and incomparable, all odd numbers are minimal and incomparable, and $2i$ covers its odd neighbors $2i-1$ and $2i+1$ (whenever the latter is present). Clearly the number of (lower) ideals is $F_{n+1}$ and the set $\mathrm{J}\big( \mathcal{Z}_n \big)$ of all (lower) ideals ordered by inclusion will be a distributive lattice.

Maybe I'll add more later, ines.

Answer 8

Integer partitions, http://oeis.org/A000041

• dominance order

Answer 9

$\binom{n}{k}$ objects, i.e., $k$-element subsets of $[n]$

• the interval $[\varnothing,(n-k)^k]$ of Young's lattice of partitions - this is a distributive lattice

Answer 10

All $2^n$ subsets of $[n]$

• Boolean lattice - (distributive)
• the interval $[\varnothing, (n,n-1,...,1)]$ of the shifted version of Young's lattice, this is the same as the dominance order on compositions of $n+1$ - (distributive)

Answer 11

Excerpt from "Distributive lattices, polyhedra, and generalized flows" by Stefan Felsner and Kolja Knauer:

Many researchers have constructed distributive lattices on sets of combinatorial objects, e.g.,

• domino and lozenge tilings of plane regions ([23] and others based on [27]).

• planar spanning trees ([11])

• planar bipartite perfect matchings ([16])

• planar bipartite d-factors ([8,22])

• Schnyder woods of planar 3-connected graphs ([4])

• Eulerian orientations of planar graphs ([8])

• α-orientations of planar graphs ([8,7])

• circular integer flows in planar graphs ([15])

• higher dimensional rhombic tilings ([18])

• c-orientations of graphs ([22]).

---

---

Perhaps you would find this answer by Vijay D to a MO-Q on dualities informative.