With the clarification given in the comments, what you are asking is if there is a bound on $d_{GH}(M, M_\sigma)$ which tends to $0$ as $\sigma\to 0$. This question has negative answer. An example is given by $M$ which is the comb space:
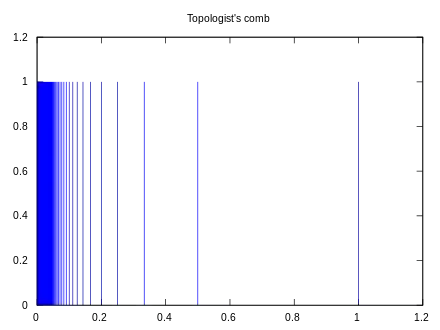
The thing is that for each $\sigma=1/n$, $M$ contains a pair of points $p=(0,1), q=(\frac{1}{n},1)$ such that
$$
d_{M_\sigma}(p,q)=1/n,
$$
while $d_M(p,q)= 2+ \frac{1}{n}$. The existence of these pairs of points prevents the GH-convergence $M_\sigma\to M$. (The space satisfies other conditions in your question: $diam(M)=3$, one can take $s=\sqrt{2}, \epsilon=3$.)
One way to define the GH distance is via distortion of bisurjective correspondences:
Definition. Let $A, B$ be compact metric spaces and $R\subset A\times B$ be a bisurjective correspondence meaning that its projection to both $A$ and $B$ is surjective: For every $a\in A$ there is $(a,b)\in R$ and for every $b\in B$ there is $(a,b)\in R$. Define the distortion of $R$ by:
$$
dis(R):= \sup_{(a,b), (a',b')\in R} |d(a, a')- d(b,b')|.
$$
Then $$d_{GH}(A,B)= \frac{1}{2}\inf_R dis(R)$$ where the infimum is taken over all bisurjective correspondences as above. Up to a uniform factor (which is irrelevant for our purposes), $d_{G}$ can be defined using $\epsilon$-surjective maps:
$$
\inf \{dis(f), f: A\to B \ \hbox{is $\epsilon$-surjective}\},
$$
where $dis(f)= \sup \{ |d(f(a), f(a'))- d(a,a')| : a, a'\in A\}$ and $f$ is $\epsilon$-surjective if each $b\in B$ is within distance $\epsilon$ from some $f(a)$.
In other words, if $dis(f)\le \epsilon$ then $f$ is a $(1,\epsilon)$-quasiisometry:
$$
d(a,a')-\epsilon \le d(f(a), f(a'))\le d(a,a')+\epsilon,
$$
Therefore, a sequence of compact metric spaces $M_n$ converges to a metric space $M$ if and only if there is a sequence of $(1,\epsilon_n)$-quasiisometries
$$
f_n: M_n\to M,
$$
which are $\epsilon_n$-surjective and $\lim_{n\to\infty}\epsilon_n=0$.
What you get in your setting is different: The inclusion map $f: M\to M_\sigma$ defines (when $\sigma\le s/3$) a quasi-isometry $M\to M_\sigma$:
$M$ is $\epsilon$-dense in $M_\sigma$ and $f$ satisfies (for all $a, a'\in M$)
$$
\frac{\sigma}{\epsilon}d_M(a, a') - \sigma\le d_{M_\sigma}(f(a), f(a'))\le d_M(a, a').
$$
The multiplicative (Lipschitz) factor $\frac{\sigma}{\epsilon}\ne 1$ in the LHS makes all the difference. This is the difference between the GH distance and quasi-isometries mentioned by in Henry's comment. The attempt to estimate (from above) the GH distance made in your post will also result in a map with such multiplicative factor $\ne 1$ and that just is not good enough. One can define a measure of closeness between compact metric spaces using quasi-isometries instead of the GH-distance. I do not know if it is useful for anything. If you are content with, say, $C^2$-smooth compact submanifolds $M$ instead of general compact subspaces then, indeed, you get GH-convergence $M_\sigma\to M$.
For more on the topic, see this question and
Burago, D.; Burago, Yu.; Ivanov, S., A course in metric geometry, Graduate Studies in Mathematics. 33. Providence, RI: American Mathematical Society (AMS). xiv, 415 p. (2001). ZBL0981.51016.
There are several other questions one can ask along the lines of your post. The more interesting of these is:
Do not fix the dimension of the ambient Euclidean space, but assume that the extrinsic diameter of $M$ is $\le D$. Is there a uniform upper bound on
$$
\liminf_{\sigma\to 0+} d_{GH}(M, M_\sigma)
$$
in terms of $s, \epsilon$ and $D$? This question also has a negative answer but examples are harder; they use the comb space as one of the building blocks.
The reason to use the extrinsic diameter is that if the intrinsic diameter is bounded by $D$ then, trivially,
$$
d_{GH}(M, M_\sigma)\le D+\sigma,
$$
which you find uninteresting. If the extrinsic diameter of $M$ is bounded by $D$ and the ambient dimension $n$ is fixed, one again obtains an upper bound on the intrinsic diameter of $M$ in terms of $D$ and $n$.
Edit. Here is a correct phrasing of your question:
- Suppose that $M\subset {\mathbb R}^n$ is a rectifiably-connected subset, such that, when equipped with the intrinsic path-metric $d_M$, $M$ is compact. Does it follow that the family of neighborhoods $M_\sigma$ of $M$ (also equipped with the intrinsic path-metrics) converge to $M$ in the GH topology?
- Suppose that $M$ is a compact connected $C^1$-smooth submanifold in ${\mathbb R}^n$. Is $M$ still compact with respect to its intrinsic path-metric?
- Suppose that $M$ is a compact connected $C^2$-smooth submanifold in ${\mathbb R}^n$. Can one estimate $d_{GH}(M, M_\sigma)$ in terms of intrinsic and extrinsic differential-geometric invariants of $M$?
Now, this question has positive answer:
Consider the identity embeddings $f_\sigma: M\to M_\sigma$. Then each $f_\sigma$ is $\sigma$-surjective and 1-Lipschitz. Thus (see the interpretation of GH distance above in terms of maps), we just need to prove that
$$
\lim\sup_{\sigma\to 0+} \sup_{p,q\in M} |d_M(p,q)- d_{M_\sigma}(p,q)|=0.
$$
A proof is by contradiction: If this limit is $\delta>0$, then (by compactness!) there are sequences $p_i, q_i\in M$ converging to $p, q\in M$ (with respect to the topology given by its path-metric) such that
$$
\lim_{i\to\infty} (d_{M_{1/i}}(p_i,q_i) - d_M(p_i,q_i))=\delta.
$$
Let $c_i: [0,1]\to M_{1/i}$ be nearly geodesic paths connecting $p_i$ to $q_i$. These paths can be taken uniformly Lipschitz (with respect to the Euclidean metric) since the diameter of $M_{1/i}$ is $\le diam(M)+ 2$. By applying Arzela-Ascoli theorem combined with the Lebesgue dominant convergence theorem, we obtain a limit path $c$ in $M$ connecting $p$ to $q$ whose length is $\le d_M(p, q)-\delta$. A contradiction.
For $C^2$-smooth submanifolds, it is a classical fact proven in pretty much every Riemannian geometry textbook that for a $C^2$-smooth Riemannian metric, the manifold topology agrees with the topology given by the Riemannian distance function. For a $C^1$-smooth submanifold, you can argue instead as follows. It suffices to show that $(M, d_M)$ is sequentially compact. By the compactness of $M$ (with the subspace topology), it suffices to show that if $p_i\to p$ in the subspace topology of $M$, then $d_M(p_i, p)\to 0$. Writing the induced Riemannian metric in local $C^1$-coordinates, it becomes merely continuous but this is enough.
(Actually, one needs even less than continuity.) The proof now becomes just a calculus computation:
$$
\lim_{i\to\infty} \int_{0}^{\epsilon_i} \sqrt{g(c_i'(t), c_i'(t))}dt \le \lim_{i\to\infty} K \epsilon_i =0,
$$
where $g$ is a continuous Riemannian metric on a domain in ${\mathbb R}^k$, $c_i: [0, \epsilon_i]\to {\mathbb R^k}$ are arc-length parameterizations of line segments (emanating from the origin) of length $\epsilon_i$, satisfying $\epsilon_i\to 0$. The constant $K$ is an upper bound on the $g$-norm of unit vectors in ${\mathbb R}^k$ near the origin. (Hence, all what you need is that, in the local coordinate, the metric $g$ is measurable and locally bounded on unit vectors, where unit is understood with respect the Euclidean norm.)
An estimate for $C^2$-smooth compact submanifolds can be given in terms of the 2-nd fundamental form (you need it for submanifolds of arbitrary codimension):
If $\sigma$ is sufficiently small (less than the normal injectivity radius of $M$ in ${\mathbb R^n}$), you have a well-defined nearest-point projection $r_\sigma: M_\sigma\to M$. You need is to estimate the Lipschitz constant $L$ of $r_\sigma$. The estimate is essentially the same as the one for the circle example:
$$
L^{-1} \ge 1- \sigma C,
$$
where, up to some multiplicative constant depending only on the dimension $n$, $C$ is the supremum-norm of the 2nd fundamental form of $M$. (In the circle example, $1/C$ is the radius of the circle.) Thus, for $p, q\in M$, you have
$$
0\le d_M(p, q)- d_{M_\sigma}(p,q)\le CD\sigma.
$$
Thus (up to a uniform multiplicative constant depending only on $n$),
$$
d_{GH}(M, M_\sigma)\le CD\sigma,
$$
if $\sigma$ is less than the normal injectivity radius of $M$.
