Showing that the inverse of a function is approximately equivalent to $\frac{1}{n^{1/\alpha}}$

Question

I'm currently working with someone on my PhD, and last week they asked me to check that a certain approximation holds as an exercise. Unfortunately, I couldn't figure out how to do it, and we've since moved on as we don't have time to go back and look at this, but it's still really bugging me.

The set up:

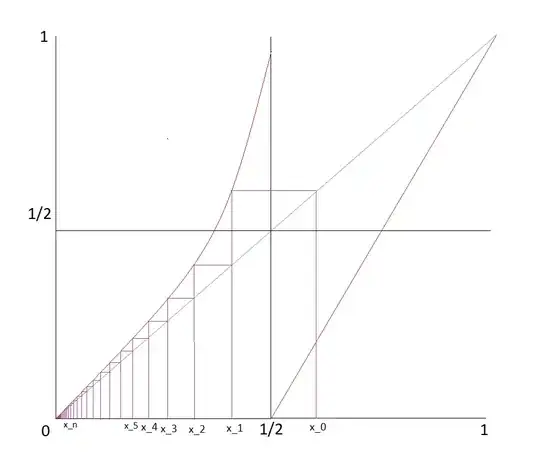
We have a piecewise map $f_\alpha: [0,1] \to [0,1]$ defined as \begin{align} f_\alpha(x) = \begin{cases} x(1 + (2x)^\alpha), &x \in [0, 1/2] \\ 2x - 1, &x \in (1/2, 1) \end{cases} \end{align} with $0 < \alpha < 1$.

Say we have a starting point $x_0$. We denote by $x_1$ the point in $[0,1/2]$ that is mapped by the left part of the map to $x_0$. We then define a sequence {$x_i$} such that $x_{n+1}$ is the point in $[0,1/2]$ that maps to $x_n$.

What I was asked to show was \begin{align} \frac{1}{2}|x_n| \sim \frac{1}{n^{1/\alpha}} \end{align}

The problem is I don't know how to go about showing this. I was hoping I could write something of the form $|x_n - \frac{1}{n^{1/\alpha}}|$ and show that it converges to zero. However, I can't explicitly express the inverse of the LHS of the function, so I can't explicitly define $x_n$ given $x_{n-1}$. Would showing that it diverges in the forward direction work? Alternatively, am I approaching this completely wrong?

Thanks in advance.

Answer 1

The right part of $f$ being not relevant, we consider the diffeo $f:[0,1/2]\to[0,1]$, $f(x)=x+2^\alpha x^{1+\alpha}$, whose inverse map $g:[0,1]\to[1,1/2]$ is strictly increasing with unique fixed point $0$, where it has the expansion $$g(x)=x\big(1-2^\alpha x^{\alpha}+o(x^{\alpha})\big).$$ (Incidentally, note that there is a power series expansion valid for $0\le x< \frac12\alpha{(1+\alpha)^{-1-\frac1\alpha}}$, that may be of use for further refinements of the asymptotic: $$g(x)=x\sum_{k=0}^\infty\frac{(-1)^k}{k\alpha +1}{k\alpha +k \choose k}(2x)^{k\alpha}=x-2^\alpha x^{1+\alpha}+(\alpha+1)2^{2\alpha} x^{1+2\alpha}-\dots$$ and for any power of $g$ as well). Since $g$ is continuous, increasing, with unique fixed point $0$, the iteration $$\cases{ x_0 \in [0,1]\\\\x_{n+1}=g(x_n)}$$ converges monotonically to $0$. Thus we have, for $n\to\infty$ $$x_{n+1}=x_n\big(1-2^\alpha x_n^{\alpha}+o(x_n^{\alpha})\big) .$$ $$x_{n+1}^\alpha=x_n^\alpha\big(1-2^\alpha x_n^{\alpha}+o(x_n^{\alpha})\big)^\alpha=$$$$=x_n^\alpha\big(1-\alpha2^\alpha x_n^{\alpha}+o(x_n^{\alpha})\big)=x_n^\alpha-\alpha2^\alpha x_n^{2\alpha}+o(x_n^{2\alpha}). $$ $$\frac{x_{n+1}^\alpha}{x_{n}^\alpha}=1 +o(1).$$ $$\frac1{x_{n+1}^\alpha}-\frac1{x_{n}^\alpha}=\frac{x_{n+1}^\alpha-x_{n}^\alpha}{x_{n+1}^\alpha x_{n}^\alpha}=\frac{\alpha2^\alpha x_n^{2\alpha}+o(x_n^{2\alpha})}{x_{n+1}^\alpha x_{n}^\alpha}=\frac{\alpha2^\alpha x_n^{\alpha}\big(1+o(1)\big)}{x_{n+1}^\alpha }=$$$$=\alpha2^\alpha\frac{ x_n^{\alpha}}{x_{n+1}^\alpha }\big(1+o(1)\big)=\alpha2^\alpha +o(1).$$ Therefore summing from $1$ to $n$ $$\frac1{x_{n}^\alpha}=n\alpha2^\alpha +o(n), $$ and finally $$ x_{n} =\frac{\alpha^{-1/\alpha}}2\, n^{-1/\alpha} \, (1 +o(1)). $$

For instance, with $x_0=1$, $\alpha=1/3$ and $n=100$, Maple gives $x_n=0.000015\dots$, while $\frac{\alpha^{-1/\alpha}}2\, n^{-1/\alpha}=0.000013.$

One can also improve the above asymptotic inserting it into an expansion for $$\frac1{x_{n+1}^\alpha}-\frac1{x_{n}^\alpha}.$$

Answer 2

Writing $y_n=2x_n$ we get, $\frac{y_{n-1}}{y_n}-1=(y_n)^{\alpha}$ and $\frac{y_{n}}{y_{n+1}}-1=(y_{n+1})^{\alpha}$.

Dividing the first by second we get, $\frac{r_n-1}{r_{n+1}-1}=(r_{n+1})^{\alpha}$, where $r_n=\frac{y_{n-1}}{y_n}$.

or, $\frac{t_{n+1}}{t_{n}}=(1+t_{n+1})^{-\alpha}....(1)$

[Where, $r_n-1=t_n >0$].

Now, $f(n):=t_n$, $f'(n)=t_{n+1}-t_n$.

From $(1)$, extending the domain from natural numbers to $\mathbb R^{+}$ we write ,

$\frac{f'(x)}{f(x)}=(1+f(x))^{-\alpha}-1$.

This differential equation gives,

$x+c=\frac{1}{\alpha f}+\frac{(\alpha+1)}{2\alpha}\log(\frac{1}{f})-\frac{{\alpha}^2-1}{12\alpha}f+o(f^2)$.

Now, for large $x$, $f≈0$, hence, $\frac{1}{f}>>\log(\frac{1}{f})>>f$.

So, we get the solution $f(x)≈\frac{1}{\alpha (x+c)}$ for some $c$.

Now, $f(n)=t_n \rightarrow -\frac{y_{n+1}-y_n}{y_{n+1}}=f(n)$. As before we write

$-\frac{y'(x)}{y(x)}≈\frac{1}{\alpha (x+c)}$.

or, $\log(y(x))≈C+\log{\frac{1}{(x+c)^{1/\alpha}}}$

or, $y(x)≈A\frac{1}{(x+c)^{1/\alpha}} \\ $.