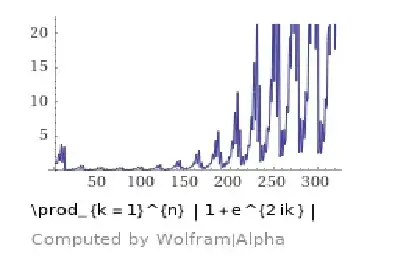
Let $$u_n=\prod_{k=1}^{n-1}\cos^2(k)$$ then $$\frac1n \ln(u_n) = \frac1n\sum_{k=0}^{n-1} \ln(\cos^2(k)) \underset{n\to\infty}\longrightarrow \frac1{2\pi} \int_0^{2\pi} \ln(\cos^2(x))\,{\rm d}x = -\ln(4)$$ We deduce that $$\ln(u_n)\sim -n\ln(4)$$ . I think that the sequence $v_n=\ln(4^n u_n))$ have not limit , So there is no constant c such that $u_n \sim c\,4^{-n}$. Can we find better then $$ \prod_{k=1}^{n-1}\cos^2(k)\sim 4^{-n}e^{o(n)}$$ . What is $\limsup 4^n u_n$ and $\liminf 4^n u_n$ ?
additional comments
wolfram does not confirm that $\liminf 4^n u_n =0$