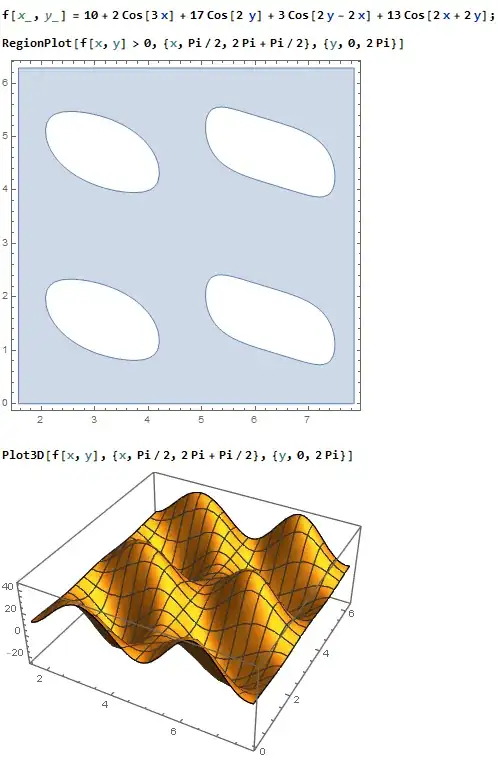
Following my previous question here, I have this function $$f(x)=10+3 \cos (ax-bx)+13 \cos (ax+bx)+2 \cos (\frac32 a x)+17 \cos (b x),$$ with $\frac ab \notin \mathbb{Q}$.
What is the limit $$ \lim_{m\to\infty} \frac 1m \int_{0}^{m} {\bf 1}[f(x)>0] \,dx?$$
Does the limit exist? Are there similar limits for functions with more terms in the sum?
Any hints and comments are appreciated.
A sample Mathematica code to find the area of the region given in Anthony Quas's comment is:
NIntegrate[
Boole[10 + 3 Cos[2 x - 2 y] + 13 Cos[2 x + 2 y] + 2 Cos[3 x] + 17 Cos[2 y] > 0],
{x, 0, 2 Pi},
{y, 0, 2 Pi}]
The output is 29.7118, but Mathematica complains about slow convergence. One can try, say:
NIntegrate[
Boole[10 + 3 Cos[2 x - 2 y] + 13 Cos[2 x + 2 y] + 2 Cos[3 x] + 17 Cos[2 y] > 0],
{x, 0, 2 Pi},
{y, 0, 2 Pi},
WorkingPrecision -> 100,
MaxRecursion -> 20]
But this does not affect neither the answer (29.7117875164...) nor the complaints.
Other ways to accomplish the same task, involving for example ImplicitRegion, do not seem to work any better.
While Mathematica's command NIntegrate[] will likely produce an output with a few correct digits, it will not guarantee any of them.
To get such a guarantee, you can partition the square $[0,2\pi]\times[0,2\pi]$ into a grid of $n\times n$ smaller congruent squares (with $n$ equal, say, $50$). On each smaller square, use a Taylor expansion of the cosine function, with a controlled remainder, to bound each of the four cosine terms in the expression of the integrand (say $f$) by a polynomial. Using then (say) Mathematica's Reduce[] command will give you a constant sign of $f$ on each of most of the smaller squares, with a few exceptions. Repeat this procedure on each of the remaining exceptional smaller squares. Continue doing so until the total area of the still remaining exceptional small squares is small enough to be considered negligible.
Visual guides for this procedure could be of help:
In particular, a useful fact that seems to have been overlooked is that the smallest $y$-period of $f(x,y)$ is of course $\pi$, rather than $2\pi$.
Using Anthony's suggestion it should not be difficult. Here is very straightforward Matlab code. This should illustrate the general method. One can of course change the function and also tune details like how the evaluation points are chosen, how many, and so on.
function beat(a,b)
% Method 1: Just take a long interval.
M = 2000*pi;
N = 1e8;
x = linspace(0,M,N);
mean(f(x,a,b) > 0)
% Method 2 (Anthony Quas): Sample random points
% from the [0,2pi]^2 torus, and do Monte Carlo integration.
s = unifrnd(0, 2*pi, 1, N);
t = unifrnd(0, 2*pi, 1, N);
mean(g(s,t,a,b) > 0)
end
function result=f(x,a,b)
result = 10+3cos(ax-bx)+13cos(ax+bx)+2cos(3/2ax)+17cos(b*x);
end
function result=g(s,t,a,b)
result = 10+3cos(2s-2t)+13cos(2s+2t)+2cos(3s)+17cos(2t);
end
