4

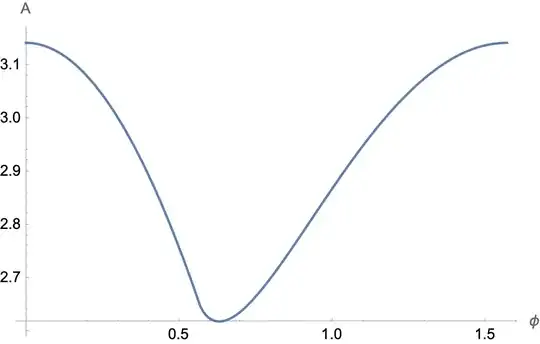
By shadow we mean the orthogonal projection of a convex 3D body P onto a 2D plane, for example, the shadow on the xy-plane, with P above (z>0) that plane and the light at L=(0,0,+∞). P an be freely rotated as it hovers above the xy-plane. Special shadows include those maximizing/minimizing various properties such as area, perimeter,..

Question: Given any convex body P, are there relationships between its special shadows and its planar sections? For example, can one assert that say, the shadow of P with the smallest area is congruent to some planar section of P?

Nandakumar R
  • 5,473
  • 1
    This might be easier to solve first for projections of 2D convex shapes onto a line. – user7868 Aug 28 '21 at 05:47
  • 1
    This is true in 2-d: Let the convex body be C. Assume wlog that the projection with smallest area is from (x,y) to (x,0), and that the projection goes from (0,0) to (1,0). Let A={y: (0,y) in C}. Let B={y: (1,y) in C}. If A and B do not intersect, let s be a point which separates them. Then C stays between the lines y=mx+s, y=m(x-1)+s for some non-zero m, and the corresponding projection is smaller than the projection from (0,0) to (1,0). This is a contradiction, so A and B must intersect. Let y be in the intersection; then the line from (0,y) to (1,y) is the section we were looking for. –  Aug 28 '21 at 08:40
  • In 2D : If we consider the light source at (0,+∞) and P being a convex polygonal region on xy plane that gets projected onto the x axis (with P able to rotate only about a line parallel to z axis), then, the shadow of P is always bounded by two lines parallel to y axis and touching P; the line segment joining the points of tangency is always a section of P due to convexity (by section, we mean the intersection of a line with P). So, the situation looks much simpler in 2D. – Nandakumar R Aug 28 '21 at 17:49

1 Answers1

4

The shadow of $P$ with the smallest area is not always congruent to some planar section of $P$. To construct a counterexample consider a double cone with radius 1 and height $h=\pi/2$. The maximal shadows have area $\pi$, and the minimal shadow area can be calculated to be close to 2.61784. It occurs at a tilt angle where the shadow of the tip is visible, such that the shadow is the union of an ellipse and a triangle which corresponds to no planar section. The continuous case of a cone can be approximated by convex polyhedra, which provide finite counterexamples for sufficiently fine approximation.

If the condition for visibility of the cone tips, $h \tan \phi >1, $ is fulfilled and $\alpha = \arcsin 1/(h\,\tan \phi)$, the area of the shadow is given by $$ 2 ( h\,\cos \alpha \, \sin \phi +\alpha \cos \phi),$$ otherwise it is $\pi \, \cos\phi$. Here $\phi$ is the angle between view direction and cone axis.

In the above minimum $\phi=0.631336$ and $h \tan \phi = 1.14851. $

Joseph O'Rourke
  • 149,182
  • 34
  • 342
  • 933
Karl Fabian
  • 1,546
  • Nice! Although I don't doubt your claims, may I ask: How did you arrive at this conclusion? "the minimal shadow area can be calculated ..." Is this empirical, or a proof? – Joseph O'Rourke Aug 28 '21 at 22:10
  • @JosephO'Rourke: The formula for the area is given above. Here is the Mathematica code : Shadow[h_, p_] := Module[{al = ArcSin[Cot[p]/h]}, If[ h Tan[p] >= 1, 2 ( Cos[al] h Sin[p] + al Cos[p]), Pi Cos[p] ]]; hh = Pi/2; Plot[ Shadow[hh, p], {p, 0, Pi/2}]; Graphics3D[{Cone[{{0, 0, 0}, {0, 0, -hh}}, 1] , Cone[{{0, 0, 0}, {0, 0, hh}}, 1] }, Boxed -> False, ViewProjection -> "Orthographic"] – Karl Fabian Aug 28 '21 at 23:37
  • 1
    The minimum is then calculated by fm = FindMinimum[ Shadow[hh, p], {p, 0.6}] – Karl Fabian Aug 28 '21 at 23:43
  • 1
    Added a graph that shows the min $\phi$. Quite clear. – Joseph O'Rourke Aug 29 '21 at 00:01
  • @JosephO'Rourke: Thank you. Maybe the area formula becomes more transparent when noting that $\alpha$ in Keplerian coordinates corresponds to the eccentric anomaly at the intersection point of ellipse and its tangent through the tip projection. The total area of the ellipse sectors is then $2 \alpha \cos \phi$ and the other terms are the areas of the two central quadrilaterals with vertices origin, tip projections and tangent intersection points. – Karl Fabian Aug 29 '21 at 04:49
  • Thanks very much... very nice example!! It now appears that finding the least area shadow of a polyhedron could be a difficult algorithmic problem. – Nandakumar R Aug 29 '21 at 07:53
  • And hope this discussion also generates examples/counterexamples for possible subcases of the question other than min area shadow – Nandakumar R Aug 29 '21 at 08:10
  • 1
    @NandakumarR: McKenna, Michael, and Raimund Seidel. "Finding the optimal shadows of a convex polytope." In Proceedings 1st Annual Symposium on Computational Geometry, pp. 24-28. 1985. $O(n^{d-1})$ for $n$ facets in dimension $d$. – Joseph O'Rourke Aug 29 '21 at 11:06