Let $f$ be a smooth and strictly concave function on $[0,1]$, where $f(0)=f(1)=0$.
Let $F_n(x)=\underset{k=0}{\overset{n} \sum } \exp(nf(\frac kn))x^k$.
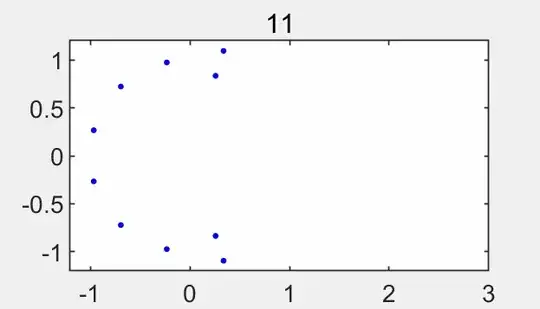
The roots of $F_n$ seems to form "shapes", for example, when $f(x)=\log(1+x(1-x))$:
Question: Given $f$, how to find out the "shapes"?
Motivation: Consider a statistical mechanics model on $n$ sites, where each site can take two states. If the function $f(x)$ is the entropy per site when proportion $x$ of the sites take the first state, then the function $F_n$ is the generating function of the number of configurations with respect to the number of sites taking the first state.