Given the skeleton of an inscribed polytope. If I move the vertices so that no edge increases in length, can the circumradius still get larger?

Question

Let $P\subset \Bbb R^n$ be an inscribed convex polytope, that is, all its vertices are on a common sphere of radius $r$. Let $G$ be the edge-graph of $P$. For convenience, assume $V(G)=\{1,\dotsc,s\}$. Let $\ell_{ij}$ denote the length of the edge of $P$ corresponding to $ij\in E(G)$.

Question. Let $p_1,\dotsc,p_s\in\Bbb R^{m}$ be points so that

• the points are on a common sphere $S$,
• $\lVert p_i-p_j\rVert\le\ell_{ij}$ for all $ij\in E(G)$,
• the center of $S$ lies in the convex hull $\operatorname{conv}\{p_1,\dotsc,p_s\}$.

Is it then true that the radius of $S$ is at most $r$? If no, does this change if $n=m$?

In other words, are the skeleta of inscribed polytopes "as expanded as possible" for the given edge-lengths?

Note that the condition on the convex hull is necessary. Without this we could choose an arbitrarily large sphere $S$, and place all the $p_1,\dotsc,p_s$ in an arbitrarily small patch of $S$, so that $S$ is their circumsphere.

---

The case $n=m=2$

I will demonstrate my general ideal on the case $n=m=2$, which I hope to somehow generalize to all cases with $n=m$. I do not yet have an idea for $m>n$.

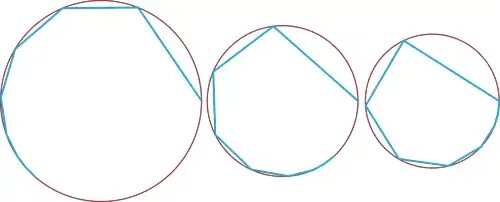
Let $P\subset\Bbb R^2$ be an inscribed polygon with circumradius $r$ and vertices $v_1,...,v_s$ in circular order. Let $\alpha_i$ be the angle between $v_i$ and $v_{i+1}$ (indices mod $s$) as seen from the circumcenter. Then $\alpha_1+\dots+\alpha_s=2\pi$.

Suppose now that we have such a set of points $p_1,...,p_s$ with circumradius $r'>r$. Let $\beta_i$ be the angle between $p_i$ and $p_{i+1}$ as seen from the circumcenter. Since $\|p_i-p_{i+1}\|\le \|v_i-v_{i+1}\|$ but also $\|p_i\|>\|v_i\|$ it is easy to see that $\beta_i<\alpha_i$. In particular, $\beta_1+\cdots+\beta_s<2\pi$, and the closed polyline with vertices $p_1,...,p_s$ must have zero winding number around the circumcenter. But since the convex hull of the $p_i$ contains the origin, there are three points $p_{i_1},p_{i_2},p_{i_3}$ with $i_1<i_2<i_3$ so that already the convex hull of these contains the circumcenter. It is then easy to see that $$\beta_{i_1}+\cdots+\beta_{i_2}+\cdots+\beta_{i_3}\ge \pi$$ and $$\beta_{i_3+1}+\beta_{i_3+2}+\cdots+\beta_{i_1-1}\ge \pi,$$ in contradiction to $\beta_1+\cdots+\beta_s<2\pi$. $\;\square$

To generalize this, one would need to find a suitable notion of "winding number" (mapping degree) for point arrangements with $n>3$, somehow using the face structure provided by the polytope. One might then be able to construct a similar argument using space angles (aka fractions of the sphere, as described by Matt F. in the comments).

Answer 1

The answer to the question is unfortunately no, in the case of $n=m=3$. There is a simple example to illustrate this.

Let $P$ be the cube with vertices $(\pm \frac{1}{2},\pm \frac{1}{2},\pm \frac{1}{2})$. Very obviously, every edge is of length $1$, and a quick calculation shows this is inscribed upon a sphere of radius $\frac{\sqrt{3}}{2}$.

We now describe the locations of 8 vertices, one for each sign-string of length 3. Vertex $V_{sign}$ with $s=\#$positive entries of $sign$ is at the point $(sin(\frac{s\pi}{3}),cos(\frac{s\pi}{3}),0)$. It is easy to check that the lengths of the edges is exactly preserved. However, these vertices lie on a sphere of radius $1 > \frac{\sqrt{3}}{2}$.

There are three things wrong with this example, two of which are immediately fixable. First, $\vec{0}$ is not interior. A small reduction of the radius can fix this. Secondly, the convex hull of these points is not full dimensional. Again a small reduction of the radius combined with some small perturbation in the third coordinate fixes this.

Finally, the images of the faces of $P$ form a complex which does not contain the origin. This is both what allows the example to exist, and makes it a not satisfying example. Perhaps an additional condition which could contribute to a winding number argument could be: the cone generated by all edges incident to a vertex contains the origin. This could replace that the origin is in the convex hull of the points.

Answer 2

This addresses only the $n=m=2$ case.

Break the polygon $P$ into an open polygonal chain with the same lengths as $P$. Place the chain in a large-radius circle, and shrink the radius until the chain closes. The result is the unique circumcircle for the inscribed $P$:

To reach closure, each $\ell_k$ must be less than the sum of the other lengths.

(This figure is from an MSE question of mine.)

Answer 3

"Yes" for the case $m=n=3$. I will assume that center of sphere lies in the first polyhedron, say $Q$, but it is straigthforward to remove this assumption.

Assume contrary. By rescaling the second polyhedron, say $P$, we can assume that the radius of the sphere stays the same as for the original polyhedron $Q$, but all edges get shorter.

Consider the central projection of the edges of $Q$ to the sphere. Note that they cut the sphere into cyclic polygons. Choose an edge $e$ of $Q$, consider two of its adjacent spherical cyclic polygons $F$ and $G$. The vertices of $F$ and $G$ lie on two arcs with endpoints of $e$. Since $Q$ is convex the arcs bound a nonconvex region from the sphere with $F$ and $G$ inside. The last statement (with some work) implies the following: if one decreases the edge $e$ while keeping $F$ and $G$ cyclic, then the total area of $F$ and $G$ decreases.

Now, for each edge of $Q$ draw a line segment between the corresponding vertices of $P$. Project the obtained line segments to the sphere. Since the center of sphere is inside of $P$ the spherical polygons that correspond to facets of $Q$ will cover the whole sphere. Note that cyclic polygon maximize the area among all polygons with the same sides. From above it follows that the total sum of their areas get smaller, but they cover the same sphere --- a contradiction.