Cutting a spherical surface into mutually non-congruent pieces of equal area

Question

Question: For what values of integer $n$ can the surface of a sphere be partitioned into $n$ convex and mutually non-congruent pieces of same area? (convexity could be viewed as geodesic convexity). If such a partition exists for some $n$'s, one can ask if one can achieve a 'fair' convex partition - pieces with same area and same perimeter - for some of those n's.

Note: one can replace sphere by general ellipsoids or tori or polyhedrons.

Speculation: Even a negative result like: "the spherical surface (or maybe even any ellipsoid or say, toroid) cannot be cut into any number of mutually non-congruent convex pieces of same area (or for that matter, 'same area and same perimeter')" could be interesting.

Answer 1

First we observe that on the sphere, the boundary between two pieces must be an arc of a great circle – otherwise one of the pieces would not be convex.

With $n = 2$ it is obviously impossible; each piece is bordered by only the other piece, so the boundary is a single great circle, and the piece is a hemisphere.

With $n = 3$ it is also impossible. Consider one of the pieces. Its borders with the other two pieces are arcs of great circles; but if you take any two great circles, they will intersect at two antipodal points. (For completeness, let us note that any two pieces $A$ and $B$ must have a single continuous boundary, not two or more separate stretches, because each piece must be connected.) So the piece you are looking at is a lune with $1/3$ of the area of the sphere. So are the other two, so all three are necessarily congruent.

With $n \ge 5$, the partitioning is possible. This is the idea:

Choose a latitude $\phi \in ]0, 90^\circ[$. Place $n-2$ points at the northern latitude $\phi$ at equidistant meridians, and connect them with arcs of great circles, going around the north pole. Likewise, place another $n-2$ points at the southern latitude $-\phi$ at the same meridians, and connect them going around the south pole. Connect each northern point to its southern counterpart along the meridian.

Consider the $n-2$ quadrilateral areas bounded by the meridians and the circumpolar arcs; and the two polar caps. By construction the quadrilaterals are congruent to each other. Now choose $\phi$ so that the two polar caps have the same area as the quadrilaterals. Here's a picture with $n=8$: six quadrilaterals and two polar caps.

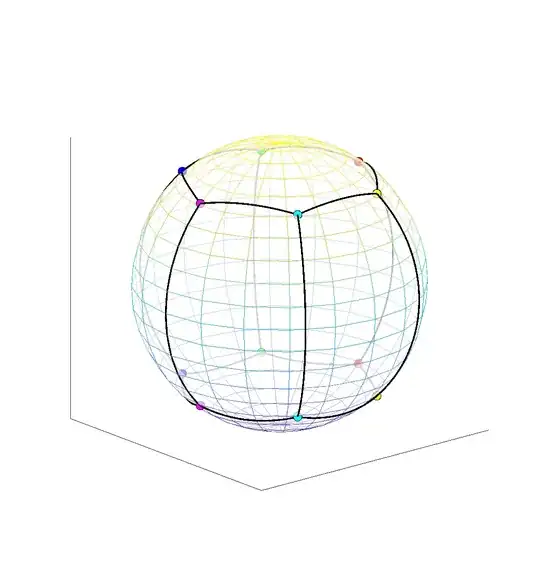
So far we have $n$ equal-area pieces. But the trouble is that the quadrilaterals are congruent.

Now make small perturbations to the vertex coordinates, such that each northcap corner is moved slightly north or south, and its southcap counterpart is moved the same amount in the same direction. This should keep the quadrilateral areas approximately unchanged. Make sure the perturbations even out, so that the area of each polar cap is unchanged.

This way, the areas are approximately preserved but the pieces will be incongruent.

A back-of-envelope calculation suggests that we have enough degrees of freedom to perturb the regions so that the areas match exactly: We have $2n-4$ vertices, each of which we can move in two directions; and we only need to match the $n$ areas (to $4\pi/n$ each).

Numerical solution

Let's then try the perturbation method numerically. We use $n=8$ as an example.

Step 0. We start with the regular congruent-quadrilaterals solution described above.

Step 1. The northcap latitudes are perturbed by different, linearly spaced values going from $-10^\circ$ to $+10^\circ$. With $n=8$ the perturbations are thus $-10, -6, -2, +2, +6, +10$ degrees, with a separation of $s=4^\circ$. Their southern counterparts are moved similarly. The areas are now inequal: they range from $1.554104736$ to $1.592563459$ (maximum difference $0.0385$).

Step 2. Using MATLAB nonlinear optimization fmincon, allowing each latitude and longitude to move at most $s/8 = 0.5^\circ$ around the initial perturbation, we minimize the sample standard deviation of the $n$ areas. For numerical optimization we set the tolerance on this cost function as $10^{-6}$.

We find a numerical solution where the $n$ areas range from $1.570796337$ to $1.570796319$, max difference $1.8 \cdot 10^{-8}$. The solution has the following latitudes and longitudes, in degrees:

$$ (35.888836,-0.397233), (40.097031,60.117286), (44.017392,120.069211), (47.997889,179.902120), (52.044716,239.869411), (55.780336,300.331731), (-55.782161,-0.338827), (-52.047816,60.120342), (-47.999809,120.083417), (-44.016062,179.913672), (-40.094474,239.865924), (-35.887467,300.382088), $$

Observe that (by construction) all northern latitudes are different, and they increase along with longitude, so all pieces are incongruent.

This is a picture of the $n=8$ numerical solution. The first northcap vertex (red) has the largest southward perturbation, and you can see how the vertices spiral towards north when going east.

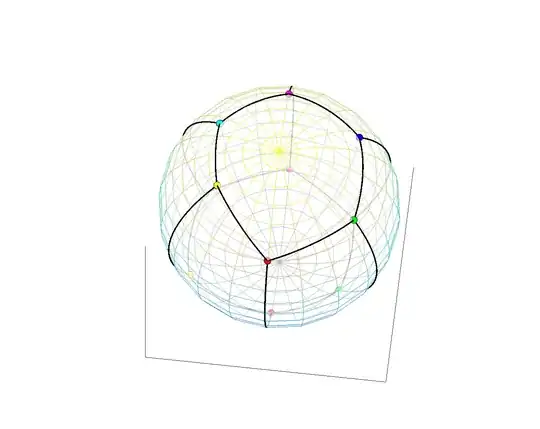
Applying the same method for any $n\ge 5$ is straightforward. I tried with various values like $n=5,6,\ldots,12$ and always got equal areas, up to the numerical tolerance. Just one caveat: If $n$ is large, then the polar caps have extremely obtuse angles; to make sure that the caps remain convex, the vertex perturbations must be small enough. But this is easy to ensure (even by trial and error).

Answer 2

There is no solution for $n=4$, by the following result.

Proposition. If $ABC$ is a spherical triangle of area $\pi$, then there is a partition of the sphere into four copies of $ABC$, and that is the unique partition into four triangles of area $\pi$ with $ABC$ as one of the triangles.

Proof of existence. By the relation of area and excess, the angles within $ABC$ sum to $2\pi$. So consider a point $P$ with $\angle ABP= \angle BCA$ and $BP=AC$. Then \begin{align} \angle PBC &= 2\pi - \angle ABC - \angle ABP \text{, since the angles at }B\text{ sum to }2\pi\\ &= 2\pi - \angle ABC - \angle BCA \text{, by construction}\\ &= \angle CAB,\phantom{2\pi - \angle ABC - }\text{ since the angles in }ABC\text{ sum to }2\pi. \end{align} From this equality we can prove others to show that the triangles $ABC$, $APB$, $BPC$, $CPA$ are congruent, and therefore all of area $\pi$. The final result has the following diagram —- where, because this is a sphere, the area outside the triangle is also a triangle.

Proof of uniqueness. Suppose $ABC$, $AOB$, $BOC$, $COA$ are all of area $\pi$. If $AOB \subset APB$ or $BOC \subset BPC$ or $COA \subset CPA$ then the triangle with $O$ would have area of less than $\pi$. Since this is impossible, $O$ must avoid all those inclusions, and therefore $O=P$. $\square$