Explicit triples of isomorphic Riemann surfaces

Question

Inspired by a discussion with Neil Strickland I am very interested to hear of explicit examples (one per answer, please), as follows.

---

A compact Riemann surface can be presented in many different ways. For example:

1. A smoothly embedded embedded surface in the three-sphere $S^3$.
2. A smooth projective curve (say cut out of $\mathbb{CP}^2$ by a single equation).
3. A quotient of the hyperbolic plane by some fuchsian group.

For each of these "ways" we can accept some minor modifications.

1. We prefer embeddings into $S^3$ (or the three-torus $\mathbb{T}^3$) because we want to actually "see" the surface. However giving the surface as a level-set of a nice function, or via some other nice analytical construction (for example as a minimal surface with symmetries), is also welcome.

2. I am not algebraic enough to deform the condition given in (2) - I hope some reader will suggest the correct modifications.

3. We also accept quotients of $\mathbb{C}$ by a lattice $\mathbb{Z} + \mathbb{Z}\omega$. We also accept tilings of the upper half-plane as long as the tiling has no "moduli" (or has enough explicit side conditions) so that the fuchsian group can be deduced, with sufficient amount of hyperbolic trig). We may also modify (3) in another way - for example giving square-tiled surfaces or more generally surfaces given by gluing explicitly described polygons in $S^2$, $\mathbb{E}^2$, or $\mathbb{H}^2$.

Question: Give explicit examples of pairs (or preferably triples) of isomorphic Riemann surfaces of the above types.

We first dispose of the trivial example of the sphere. Here (1) and (3') are addressed by saying "the round sphere". (2) is addressed by saying (for example) "$x + y + z = 0$".

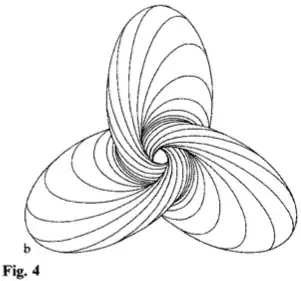
As an actual example, we have tori. For (3), we specify $\omega$ and thus the lattice $\mathbb{Z} + \mathbb{Z}\omega$. For (2), we have the Eisenstein series giving the modular invariants. For (1) we have the Hopf tori embedded in $S^3$ (and thus, after stereographic projection, embedded in three-space). Pinkall [Inventiones, 1985] defines these, and has explicit constructions (see Figure 4b (reproduced below) and Figure 6b). See also Figure 5 of Sullivan [Bridges, 2011].

I give further examples in the comments here but please see, in addition, Strickland's talk.

Answer 1

A particular example is that of the Lawson surface $\xi_{g,1}$ of genus $g$. As defined here, it is a compact minimal surface in the 3-sphere, obtained by reflecting the solution of the Plateau problem for a specific geodesic 4-gon. The surface has many symmetries, so it is easy to deduce that it is given by the algebraic equation $$y^2=z^{2g+2}-1.$$ Finally, the Riemann surface has so many symmetries that you can write down its uniformisation oper (and its monodromy) explicitly: the former is given by the desingularisation of the pull-back (by the holomorphic map to the projective line obtained by quotienting out all symmetries) of the Fuchsian system $$\nabla\,=\,d+\begin{pmatrix}\frac{1}{8}&0\\0&-\frac{1}{8}\end{pmatrix}\frac{dz}{z}+ \begin{pmatrix}-4\rho^2&1\\ \rho^2-16\rho^4&4\rho^2\end{pmatrix}\frac{dz}{z-1}$$ where $\rho=\tfrac{g}{2g+2}.$ The Fuchsian group can be computed explicitely from the monodromy of the Fuchsian system, which is (conjugated to) the representation of the 3-punctured sphere with monodromies $$ M_0\,=\,\begin{pmatrix}\frac{1}{\sqrt{2}}& -\frac{1}{\sqrt{2}}\\ \frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}} \end{pmatrix}$$ $$M_1\,=\,\begin{pmatrix} -\cos{\frac{\pi}{k}}-\sqrt{(1+\cos{\frac{\pi}{k}}) \cos\frac{\pi}{k}}& 1 + \cos{\frac{\pi}{k}}+\sqrt{(1+\cos{\frac{\pi}{k}})\cos{\frac{\pi}{k}}}\\ -1 -\cos{\frac{\pi}{k}}+\sqrt{(1+\cos{\frac{\pi}{k}})\cos{\frac{\pi}{k}}}& -\cos{\frac{\pi}{k}}+\sqrt{(1+\cos{\frac{\pi}{k}}) \cos\frac{\pi}{k}} \end{pmatrix}$$ $$M_\infty\,=\,\begin{pmatrix} \frac{1}{\sqrt{2}}&\frac{-1- 2\cos{\frac{\pi}{k}}-2 \sqrt{(1+\cos{\frac{\pi}{k}})\cos{\frac{\pi}{k}}}}{\sqrt{2}}\\ \frac{1+ 2\cos{\frac{\pi}{k}}-2\sqrt{(1+\cos{\frac{\pi}{k}})\cos{\frac{\pi}{k}}}}{\sqrt{2}}& \frac{1}{\sqrt{2}} \end{pmatrix},$$ where $k=g+1.$

A 3D print of the (stereographic projection of the) genus two Lawson surface. The (conformal) parameterisation is due to Sebastian Heller and Nicholas Schmitt - the print is due to Nicholas Schmitt and Wjatscheslaw Kewlin, and the photo is due to Wjatscheslaw Kewlin.

Answer 2

There are indeed very few pairs (except spheres with 3 or 4 singularities, or tori, and what can be obtained from them by finite coverings, where correspondence 2)-3) is completely explicit. See:

H. P. de Saint-Gervais, Uniformisation des surfaces de Riemann, ENS Editions, 2010 (there is an English translation), Chap. IX.

Concerning pairs 1)-3), many beautiful examples occur in the theory of minimal surfaces; they can be seen in the Bloomington Virtual Minimal Surface Museum.

Answer 3

A classical, wonderful example in which is possible to explicitly see all the three descriptions is the Klein quartic.