This is motivated by the new paper of Smith, Myers, Kaplan, and Goodman-Strauss, wherein they define the existence of an aperiodic monotile. Clearly their tiling is not three-colorable, so we have from Appel and Haken (1977) that its chromatic number is 4. What is not clear to me, however, is how one could algorithmically construct such a coloring. Any suggestions would be much appreciated!
-
Do you have a quick proof that three-colorability fails? It took me filling out a moderately large patch before I reached a contradiction. – RavenclawPrefect Mar 25 '23 at 03:41
-
3The three-coloring question was asked and answered at Can we three-color a tiling of the plane with Smith, Meyers, Kaplan, and Goodman-Strauss's einstein? – Gerry Myerson Mar 25 '23 at 04:37
5 Answers
I tried to find a colouring where one of the colours comprised exactly the 'flipped' tiles. So I coloured all of the flipped tiles blue and then found three of the remaining tiles which were all touching and coloured them red, yellow and green arbitrarily. After this I found that I could keep expanding the colouring by finding an uncoloured tile that was touching two of red, yellow and green, and colouring it with the third colour. I never had to make any choices, so it seems that there is a unique colouring such that one of the colours comprises exactly the flipped tiles.
If this is true then the colouring is trivial to perform algorithmically, but I don't yet have a complete proof.
Look at the reduction to an hexagonal grid shown in Figure 2.2 of the original paper.
The hexagonal grid is formed by merging each flipped tile with a neighbour. The hexagonal grid is strictly more connected than the unflipped tiles (i.e. there are hexagons that touch even though their corresponding tiles don't). So the unique 3-colouring of the hexagonal grid does indeed yield a 4-colouring of the original tiling.
It remains to show that this colouring is the unique such.
Added 2023-06-14: The new Spectre tiling does not involve any flipped tiles. However we can still produce a similar colouring. Some of the tiles are special in that their rotation is an odd multiple of $2\pi/12$ relative to the others. Colouring these tiles in blue, the remainder can again be three coloured in a unique way.
- 3,077
-
2Jesse Clark has the same colouring here: https://twitter.com/myhf/status/1639053012399439872. They didn't notice that the flipped tiles are all the same colour, but did point out that four tiles meeting at a point all have different colours. – Oscar Cunningham Mar 25 '23 at 09:16
-
-
1@MarkS If you squint a bit, you can see that the red, yellow and green tiles form hexagonal grids with the same angle and spacing, while the blue tiles form a hexagonal grid with a different angle and larger spacing. My guess would be that the constants relating the two grids are irrational, killing any wallpaper group. – Oscar Cunningham Mar 25 '23 at 15:59
-
I think it is worth to point out that the "special" tiles in Spectre tiling are not arbitrary -- in the Hat tiling, you can smoothly change a parameter to get a spectrum of aperiodic tiles; Hat and Turtle are popular ones, and Spectre is one of the shapes in this spectrum (which happens to admit different tilings if mirroring is allowed). The same operation can be done with Spectre tiling, but (except the Spectre parameter) you get two different shapes, for example, you get both Hats and Turtles. So this is where the "special tiles" come from. – Zeno Rogue Mar 14 '24 at 10:21
I think there's no obstruction to just greedily choosing a working color by going outwards in a spiral:
Each new tile never borders more than three pre-colored neighbors.
- 2,298
The bijection between non-reflected tiles and a hexagonal tiling is the way to go. To construct it, we can associated to the hat tile a corresponding hexagonal tile, so that a tiling of hats gives a partial tiling of hexagons:

This partial tiling, minus the reflected tiles, has a natural decomposition into 'triangles' constructed from hexagons, of side length 1, 2 or 3, which slide together to form a full tiling. This is probably best understood by interacting with this p5js sketch.
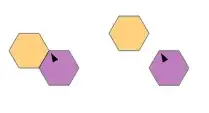
In a some more detail, write $T_{hex}$ for the hexagon associated to a hat tile $T$, and $T_{hex}^o$ for $T_{hex}$ minus its vertices, and call a tile face up if it is isometric to a rotation + translation of the tile above, and face down otherwise (likewise for the corresponding hexagons, which we'll colour purple and orange respectively). Then one can show that for a tiling $X$ of hats, each connected component of $\cup \{T_{hex}^o | T \in X, T\text{ face up}\}$ is constructed in one of the following three ways:

In addition, let arrows denote the 'triangle vertices' of the 2- and 3-triangles

Then these hexagons are adjacent or almost adjacent to reflected tiles, in the sense illustrated below.
(it turns out that the vertices of the 3-triangle are always adjacent to reflected tiles, but we do not need this fact here)
The 1-triangle is either adjacent to 3 reflected tiles, or almost adjacent to 3 reflected tiles, as illustrated below.
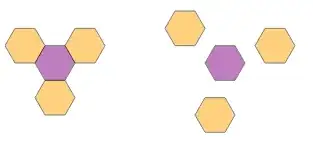
Since any partial tiling $X_{hex}$ of hexagons coming from a tiling of hats contains a face up hexagonal tile adjacent to a face down hexagonal tile, we can assume WLOG that $X_{hex}$ contains a patch of the form:

Proposition: such a patch is part of a larger neighbourhood:

Note that the 1- and 2-triangles shown above may form part of larger hex triangles.
Consider the following lines on these neighbourhoods (for convenience, we also include the patch rotated by /3).
The red and blue curves can be extended arbitrarily far in either direction. For example, moving from left to right along the red curve in patch A, we end up traversing the top edge of a 2- or 3-triangle. The top right vertex of this triangle must be adjacent or almost adjacent to a face down hexagon, which means the top edge coincides with the top edge of the triangle on the lower left of the diagram in patch A or B, respectively, and thus the red curve can be extended further to the right.
Thus we can construct three families of curves, each of which divides the hexagons into 'ribbons' indexed by $\mathbf{Z}$. We can use these indices to define translations of all hexagons that result in the simultaneous Tetris-like move in the interactive sketch linked above.
Incidentally, the orientations of $\{T_{hex} | T \text{ face down}\}$ appear to behave similarly (at least qualitatively), so there may be a hierarchy of hat and hex tilings (possibly alternating between face up and face down dominant tiles)
- 61
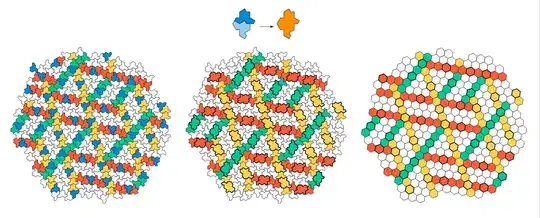
Here are some computable colorings discovered by Simon Tatham. The algorithm is described at Appendix: four-colourings of the Hats and Spectre tilings.
Hat

Spectre

- 5,715
This tiling and colouring has translation symmetry (bold dashed line) and point symmetry (red dots and thin dashed lines). No point symmetry for the tiles under the translation axis. But it cannot tile the whole plane. It's only a frieze as one cannot continue the tiling beyond the red lines. One gets holes and/or overlap. I could not keep the same colours for the flipped tiles (bold boundary) under the translation axis as Oscar Cunningham did. Here too four tiles touching one point (can) have 4 different colours (the flipped yellow tiles can as well be cyan). Perhaps that's a sufficient rule. 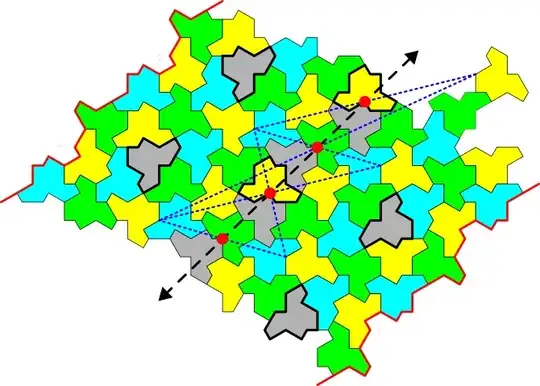
- 35
-
1The question is asking about the tiling of the whole plane, given in the reference, though. – David Roberts Mar 27 '23 at 20:48
-
-
Well, it would be useful if there were some comments that indicated how this can help address the original question, otherwise it's not clear iwhat the OP can do with this answer. – David Roberts Mar 28 '23 at 11:21
-
1Is Appel & Haken's proof still applicable to an infinite aperiodic graph ? Such a graph with 1 region less still remains an infinite graph, right? How to apply the reduction principle then? – P.Labarque Mar 31 '23 at 08:03
-
1
-
-
FWIW, it looks like @P.Labarque did so here: co.combinatorics - 4CT for infinite aperiodic planar graphs - MathOverflow – nealmcb Apr 02 '23 at 16:41
-
Perhaps that's a sufficient rule. No. That's not enough,yet. If you plot only the vertices of the larger spectre tile pattern, you can see that all the vertices are on short line segments, and not on long straight lines. There is a csv file containing 4401 vertex coordinates of specter, so please check for inadequacy. https://github.com/reversi-fun/symbolic-spectre-tiles/blob/main/spectre-tile7.3-12.6-4-4401tiles.svg.csv Spectre tiles vertices
– fun.2019 reversi Feb 28 '24 at 14:49