Non-definability of graph 3-colorability in first-order logic

Question

What is a proof that graph 3-colorability is not definable in first order logic? Where did it first appear?

Answer 1

Here is one way to do it.

2-colorability case. First let's warm up with the 2-colorability case. Notice that odd-length cycles are not 2-colorable, since the colors have to alternate as you go around the cycle, but then since it is odd length, when you get back to the starting point the parity is wrong. So take a nonprincipal ultraproduct of all finite odd-length cycles. The ultraproduct consists of nodes all of degree 2, but contains no finite cycles at all. So the ultraproduct is 2-colorable, even though none of the factors is 2-colorable, which would violate the Łoś theorem if 2-colorability were expressible.

3-colorability. For 3-colorability, now, we can do something similar. Instead of cycles, consider finite bands made of triangles like this. 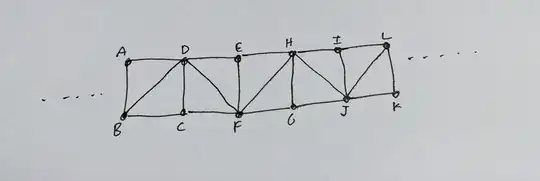Each triangle will use three different colors, and so if the whole thing was three colorable, then A will get the same color as C, and the same as E, G, I, K etc.

Now, we loop this band around to the starting point, like a giant fastening his belt. If we identify L and K with A and B, for example, then it would not be 3-colorable, since we said A must have the same color as K and different from B.

More generally, using any odd number of steps will mean that the fastened looped belt will not be 3-colorable. This is just like the 2-color case where odd cycles are not 2-colorable.

But now we can proceed as before. Take an ultraproduct of longer and longer such odd-length finite looped belts. None is 3-colorable, but the ultraproduct consists entirely of infinite belts only (since locally it looks like any big looped belt does, but since the finite looped belts grow in size, it never loops back). So the ultraproduct is 3-colorable, but no factor is.

So 3-colorability is not expressible in first-order graph theory.

Alternative argument using bicycle wheels. Emil points out in the comments that one can also use odd-length cycles with a center vertex adjacent to all nodes on the cycle, like a bicycle wheel with an odd number of spokes, and this may be a simpler way of proceeding. These are not 3-colorable, but the ultraproduct of larger and larger such wheels will consist of infinite $\mathbb{Z}$-chains attached to a center vertex, and these are 3-colorable. So 3-colorability is not expressible.

$n$-colorability. The previous idea generalizes to $n$-colorability for every finite $n\geq 2$, just by adding more nodes connected to all the earlier nodes.

Omitting ultraproducts. One can cast all the arguments via compactness instead of ultraproducts. For example, if 2-colorability were expressible, then write down the theory saying that the graph is not 2-colorable, every node has degree 2, and (as a scheme) there are no finite cycles of any particular size. This theory is finitely satisfiable, in sufficiently large odd-length cycles, but it is not satisfiable, since any model of the whole theory will consist of disjoint $\mathbb{Z}$-chains of adjacent nodes, and these are all 2-colorable. Contradiction. Similar compactness arguments work in the other cases in place of the ultraproduct.

Answer 2

It’s worth noting that Joel’s great answer says that $n$-colorability is not definable by a single sentence of first-order logic. However, it is definable by a first-order theory.. That is, for each $n \in \omega$, there is a first-order theory $T_n$ in the language of graphs so $G\vDash T_n$ iff there is a proper $n$-coloring of $G$.

I can’t actually write down the axioms of $T_n$, but you can show it exists by the Keisler-Shelah(?) characterization of elementary classes: a class of $\tau$-structures $\mathbb{K}$ is an elementary class iff it is closed under isomorphisms, ultraproducts, and ultraroots. We define $\mathbb{K}_n$ to be the class of $n$-colorable graphs. Then $G \in \mathbb{K}_n$ iff it has an expansion to add disjoint predicates $R_i, i<n$ with no two adjacent vertices in the same predicate. Crucially, these extra axioms are universal!

• Closed under isomorphism.
• Ultraproducts commute with expansion, so we can take the ultraproduct of the expansions to get the expansion of the ultraproduct. Since the extra axioms are first-order, the ultraproduct is also $n$-colorable.
• Let $G$ be a graph and $\prod G/U \in \mathbb{K}_n$ and $\left(\prod G/U\right)^+$ is the expansion. Since the new axioms are universal, they are inherited by any substructure. Since the expansion is all relations, the expansion of $G$ is a substructure of $\left(\prod G/U\right)^+$. \end{itemize} So there is some theory, but I don’t know a better way to write it down besides $T_n = \text{Th}(\mathbb{K}_n)$.

This is a specific instance of the following general principle (which I assume is folklore):

Theorem Let $T_0$ be a first-order theory in the language $\tau_0$. Let $\tau_1$ be a relational language and a $T_1$ be a universal first-order theory in the language $\tau_0 \cup \tau_1$. Then $$PC(T_0 \cup T_1, \tau_0) = \left\{ M \upharpoonright \tau_0 : M \vDash T_0 \cup T_1\right\}$$ is an elementary class.

For instance, this shows that the class of orderable graphs is also an elementary class.