2

I wonder several questions about Cayley graphs of finite Heisenberg groups H3(Z/nZ).

Question 1: do we know the diameter dependence on "n", at least for the standard choice of generators ? What about some other choices ?

Question 2: Is it true/known that the distance distribution approaches the Gaussian for large "n" ? What are the m,sigma ? What is the rate of the convergence ? (For standard generators and is something known for other choices of generators ? ).

Motivation: As far as I understand for generic non-commutative groups/their generators we can expect exponential growth at least to nearby diameter, while for commutative-like the the distribution would be Gaussian like with the mode of the distribution placed quite far from the diameter. See examples e.g. here .

Question 3: Are there some general results stating that for some class on say nilpotent groups, for their finite quotients, the distance distribution would tend to Gaussian ? (For example unitriangular/related matrices over Z/nZ).

PS

Here are some simulation for Heisenberg groups for standard and a bit-bit non-standard generators. One can find some more background/info at the head of the linked notebook.

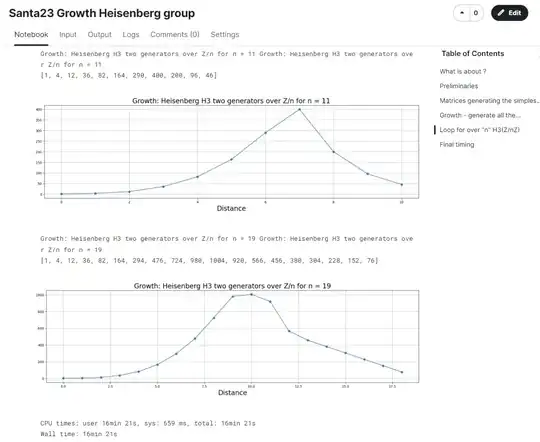
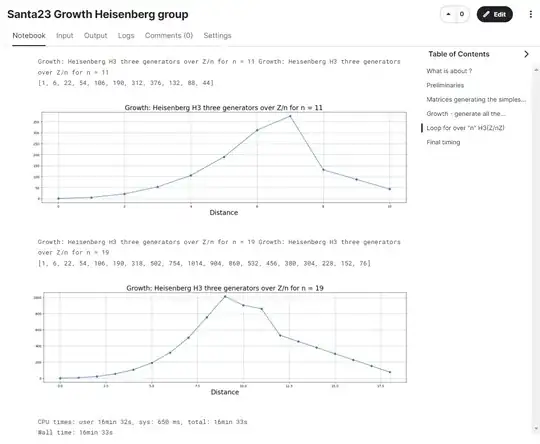
Heisenberg group with two standard generators <x,y> https://www.kaggle.com/code/alexandervc/santa23-growth-heisenberg-group?scriptVersionId=158703270&cellId=16 enter image description here

Heisenberg group with three generators (standard <x,y> and their commutator "z") https://www.kaggle.com/code/alexandervc/santa23-growth-heisenberg-group?scriptVersionId=158703218&cellId=16 enter image description here

Alexander Chervov
  • 23,944
  • Later remarks - about Guassian - it might not be correct - for abelian groups (Z/n)^d we get normal distribution for large "d" , but not "n". So here probably we get normal distribution also for Heisenberg groups of rank "d" for large "d". While H3( Z/n) for finite "n" the beginning of the sequence is the same as for H3(Z) , which generation function is - RATIOANL function https://oeis.org/A063810 : 1, 4, 12, 36, 82, 164, 294.... – Alexander Chervov Jan 15 '24 at 13:08

0 Answers0