4

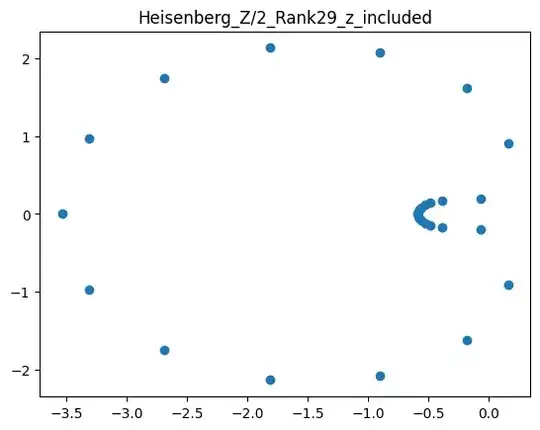
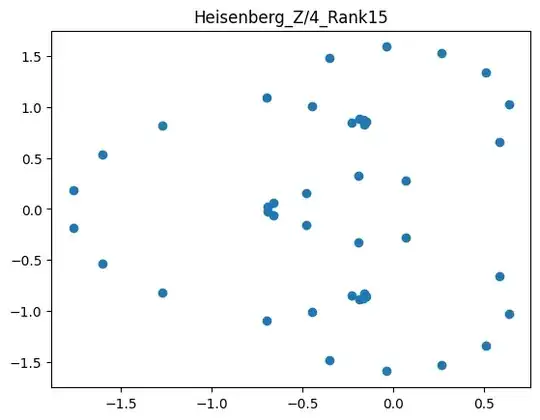
Take a standard finite Heisenberg group with two standard generators and let's consider its growth polynomial - the polynomial which coefficients are equal to the sphere sizes. For example for $H_3(Z/2)$ , polynomial is given by $p(t) = 1+2t+2t^2+2t^3+t^4$ : one element on distance zero, two elements on distances 1,2,3 and one on distance 4.

Question: Do we know the general form of these polynomials ? Are the generalizations  for the higher-dimensional Heisenberg groups known?

We have some pictures with roots of these polynomials for the different groups ( https://www.kaggle.com/code/mixnota/growth-polynomial-analysis ):

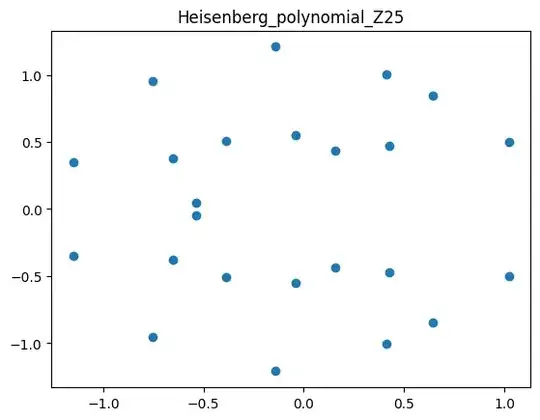
Can patterns seen on this data be helpful to guess properties of polynomials ? enter image description here

enter image description here enter image description here

PS

Googling does not help to find the answer, similar question on MSE remains unanswered: https://math.stackexchange.com/q/4868762/21498

Mikhail Evseev
  • 41
  • 2
  • It should be that $P(t) = (t^{N}P_1(t) + P_2(t) )/Q(t) $ , where $P_2(t)/Q(t)$ is growth for INFINITE $H_3(Z)$ and N is large for large "n" ($Z/n$) . (See g.f. for https://oeis.org/A063810 for $P_2(t)/Q(t)$ ) . But it is NOT clear how much $P_1(t)$ depends on "n" ($Z/n$). At least it quite might depend on n mod 2 or 4 , because n mod 2 it is already present for the more simple case of the commutative group $Z/n$. – Alexander Chervov Feb 29 '24 at 06:15
  • In the other words we hope we know the limit of $P_n(t)$ in t-adic topology - it is naturally the series for $H_3(Z)$ (i.e. $n=\infty$) , but what we miss - is the control of the error term. If error term reduces to some finite number of options (polynomial(s)) - then we can find it by just by brute force computing finite number of cases $H_3(Z/n)$ and solving linear equations. – Alexander Chervov Feb 29 '24 at 08:43
  • Surprising: "The diameter of the Cayley graph for the finite Heisenberg group over Z/n is not explicitly provided in the given sources" https://scienceos.ai/search?q=what+is+the+diameter+of+the+cayley+graph+for+finite+heisenberg+group+over+Z%2Fn If diameter is not known, then polynomial also. But may be that AI-search is not just powerful enough. Searh request was "what is the diameter of the cayley graph for finite heisenberg group over Z/n" – Alexander Chervov Mar 06 '24 at 08:07
  • With Bing AI chat: "Unfortunately, I don’t have the exact diameter for this group over (\mathbb{Z}/n\mathbb{Z}) in my current knowledge base. " https://www.bing.com/chat Query: "what is diameter of the finite Heisenberg group over Z/n" . So should be good question to benchmark AI searches :) :) – Alexander Chervov Mar 06 '24 at 12:50
  • We have counted that $N=\lceil2\sqrt{n}\rceil$ , this rule is valid for all numbers n greater than 14 for which we have calculated the growth polynomial. – Mikhail Evseev Mar 17 '24 at 15:48
  • https://link.springer.com/article/10.1007/BF01394026 M. Benson "Growth series of finite extensions of ℤn are rational" . Might be of some relevance, but not directly - because it discusses finite extension of Z^n , but we are interested in finite extension of (Z/n)^2. – Alexander Chervov Mar 18 '24 at 08:58

0 Answers0