ASCII prime plots and prime-rich quadratic polynomials

Question

This is a series of questions inspired by the MathOverflow question Find the least prime so that p-1 has two factors greater than $m$ and $n$ posted by Aaron Sterling.

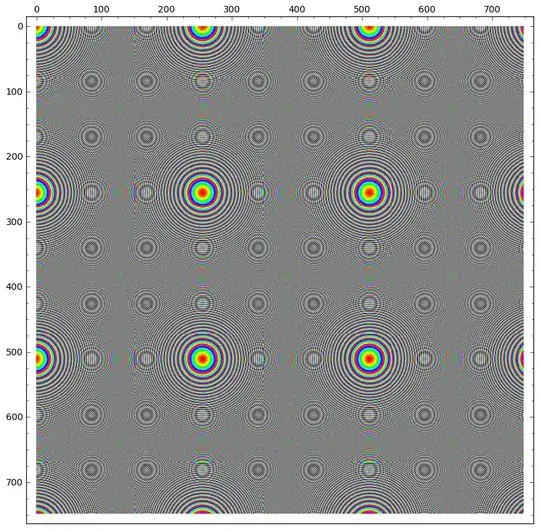
I suggested plotting primes by marking the status of the number $(nm+1)$ at coordinate $(n,m)$. Using commutativity, I have combined two ASCII art plots for $1 \leq n,m \leq 50$ in a figure-ground contrast. (Perhaps Joseph O'Rourke will be inspired to provide some similar but nicer looking plots for other ranges of $n$ and $m$.) In the plots below, + indicates $nm+1$ is prime, and other characters (after a shift in one coordinate) indicates whether $nm + 1$ has a factor of two, three or five.

+  .o.Oo .oO o .O. o Oo. oO.o. O .o.Oo .oO o .O. o Oo
++  O o  O  o Oo  oO o  O  o Oo  oO o  O  o Oo  oO o
 +   O . .O. . O . .O. . O . .O. . O . .O. . O . .O.
+ ++   oO o  O  o Oo  oO o  O  o Oo  oO o  O  o Oo  o
 +     . o .o. o .o. o .o. o .o. o .o. o .o. o .o. o
+++ ++     O    O    O    O    O    O    O    O    O
   + +   Oo. oO.o. O .o.Oo .oO o .O. o Oo. oO.o. O .o
 +  +     O o  O  o Oo  oO o  O  o Oo  oO o  O  o Oo
 + +   +   . O . .O. . O . .O. . O . .O. . O . .O. .
+ ++ ++  +   o  o  o  o  o  o  o  o  o  o  o  o  o  o
 +   + +     . oO.o. O .o.Oo .oO o .O. o Oo. oO.o. O
+ + ++ ++     O    O    O    O    O    O    O    O
   + +   + +   Oo. oO.o. O .o.Oo .oO o .O. o Oo. oO.o
 ++ +  ++    +    O  o Oo  oO o  O  o Oo  oO o  O  o
 + +     + + +   . . . . . . . . . . . . . . . . . .
+    ++    +  ++   o Oo  oO o  O  o Oo  oO o  O  o Oo
     + +     +     O o .O. o Oo. oO.o. O .o.Oo .oO o
++ + ++ +++   + +   O    O    O    O    O    O    O
         + +         .oO o .O. o Oo. oO.o. O .o.Oo .o
 ++ +   +  + +     +    o  o  o  o  o  o  o  o  o  o
 +   +   +     + + +   . .O. . O . .O. . O . .O. . O
+ ++    +     ++ ++ +   Oo  oO o  O  o Oo  oO o  O  o
 +   +     +       +     O o .O. o Oo. oO.o. O .o.Oo
  ++   + +  ++  +++    +    O    O    O    O    O
   + +   +     +       +   .o. o .o. o .o. o .o. o .o
 ++ ++     +    +  ++ +  +    oO o  O  o Oo  oO o  O
   + +   +   + + + +         O . .O. . O . .O. . O .
+  +  +  + +  ++     + ++ +   Oo  oO o  O  o Oo  oO o
 +     +   +     +             . O .o.Oo .oO o .O. o
++  +++++ +  +   ++++++ + +
         + +         +           .o.Oo .oO o .O. o Oo
  +  + +  +  +   + ++  +    +     O o  O  o Oo  oO o
 +   +   + + +     + +   +   +     O . .O. . O . .O.
  ++  + +  ++    ++       ++ +  +    oO o  O  o Oo  o
 +   + +   + +   + +     +   +       . o .o. o .o. o
+++ +     ++  +++   + +  + +  ++   +     O    O    O
   + +         +                 +     Oo. oO.o. O .o
    ++    ++  + +  +        +  +        O o  O  o Oo
 + +   +     +       + +   + + + +   +   . O . .O. .
+    ++  +  + ++  +  +       +  ++  +  +   o  o  o  o
 +               + +         +       +     . oO.o. O
+ + +  ++++ + ++ +  + ++++    +  ++  +  +   O    O
   +     +           + +     +     +   +     Oo. oO.o
 +     ++    ++    +  +     ++ ++               O  o
   + +     + +   +   +   +       + +   +       . . .
+ +  +   +  + +  +  ++  +  + ++    +     ++      o Oo
     +       +     +   + +         + +     +     O o
 + ++ + +  + + +    +  ++++   +     + +  + ++     O
   +     +       +         + +   +                 .o
 ++ +  +   + ++     + ++ +  +  +   + ++     + +

Based on this plot, I suspect my conjecture about the prime "nearest" to and greater than $n*m$ being at most $4nm$ not only holds (as a sort of 2-dimensional Bertrand's conjecture), but that this prime differs in taxicab distance by $O(\log(nm)^2)$. In other words, there is an absolute constant $C$ such that there is a prime $p$ with $p-1 = n'm'$, and with $n \leq n' \leq n + C\log(nm)^2$ and also $m \leq m' \leq m + C\log(nm)^2$. I am interested in information supporting or refuting my suspicion (and I suspect Aaron Sterling shares this interest), but that is incidental to what follows.

The primary question is a reference request: has anyone seen a plot like this before in the literature? I know of Ulam Spirals ( http://en.wikipedia.org/wiki/Ulam_spiral ) and it seems that artefacts in the plot might be related to a conjecture of Hardy and Littlewood regarding primes of the form $ax^2 +bx +c$. What I find striking are the diagonals that occur in the plot, especially those starting at $(a,a)$ and continuing in the direction $(2,-1)$. In particular, the sequence 101,109,113,113,109,101,89,73,53,29 appears as such a diagonal. Is it possible that primes of the form $a^2 + 1$ lead to prime rich polynomials of the form $(a+2t)(a-t)+1$? The secondary question series is: what is known about prime rich quadratic polynomials, and does such knowledge follow naturally from studying plots like those above?

Gerhard "Ask Me About System Design" Paseman, 2011.10.11

Answer 1

Here is a sage plot of the number of divisors of $xy$ and $xy+1$ and primality of $xy+1$ (darker is smaller):

EDIT

As Joseph O'Rourke and Gerhard Paseman pointed out, the original plots were incorrect.

The grid like structure visible in some of the plots was caused by image processing, most likely by interpolation in the shrinking.

Updated the images (and the constants in the code) to hopefully something saner.

number of divisors of $xy$: number of divisors of $xy+1$

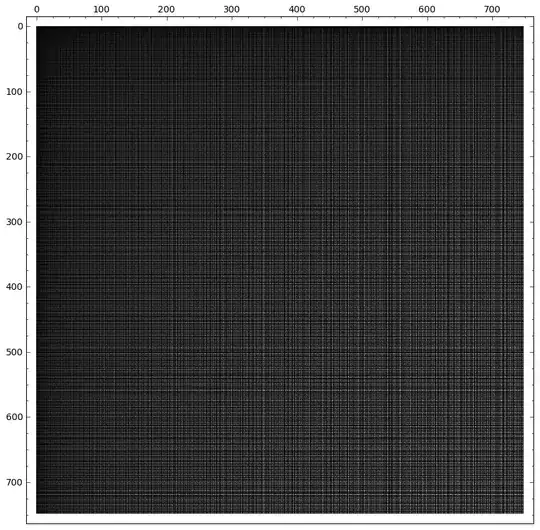number of distinct prime factors of $xy+1$:

$xy+1$ is prime:

$xy+1$ is prime zoomed:

Just for recreational purposes plot of $x^2+y^2 \mod 2^9$ in HSV colormap.

Code:

sage: lim=750
sage: D=[[ len(divisors(i*j)) for i in range(1,lim)] for j in range(1,lim)]
sage: M=matrix_plot(D,vmin=2,vmax=max(flatten(D)),cmap='gray')
sage: M.show(figsize=[10,10]) #might be dependent on dpi

for the second

sage: D=[[ len(divisors(i*j+1)) for i in range(1,lim)] for j in range(1,lim)]

Answer 2

joro's plots are much more detailed and informative, but here is a plot closer to your original ASCII art: red is prime, green is composite with no prime factor in $\lbrace 2,3,5,7,11 \rbrace$, and the other colors indicate composites with smallest factor among those primes (blue, purple, magenta, orange, yellow). The range here is $n,m \in [1,300]$, with $(1,1)$ in the lowerleft corner. I find this display relatively unrevealing, only repeating the grid-like pattern evident in joro's plots. Edit: I saved the image through a different process and the grid-like structure disappeared, pretty much confirming that the grid-pattern was an imaging artifact. This less-deceiving image is, alas, not very interesting...
           

---

To respond to joro's question, here is just primes vs. not-primes (red and white), $n,m \in [1,1000]$, which should be directly comparable to his last plot.