16

If you take a (labelled, oriented) 2 component link, it has a symmetry group which is a subgroup of the 16 element group $Z2 \times (Z2 \times Z2 \ltimes S_2)$ (mirror, reverse each component, swap the components). With Parsley, Cornish, and Mastin (http://arxiv.org/abs/1201.2722) I compiled a table of the frequency with which each conjugacy class of subgroups of this group comes up as a symmetry group for links up to 14 crossings.

Interestingly, the full group never came up as a symmetry group! Can a 2 component link ever have the full 16 element group? Is there some obstruction to this? Can anyone propose an example link?

Edit: A non split example. It is easy to construct split ones!

Clarification: The traditional symmetry group is the mapping class group $MCG(S^3,L)$. The symmetry group I want is the image of that group under the homomorphism $MCG(S^3,L) \rightarrow MCG(S^3) \times MCG(L)$, which is the 16 element group above. So another way to ask the question would be: can this homomorphism ever be surjective?

Jason Cantarella
  • 707
  • 2
    you might also want to add "non-split" to the hypotheses, to avoid the example of a split union of two copies of a reversible, amphicheiral knot. – Paul Mar 18 '12 at 04:21
  • 1
    do you mean its symmetry group surjects a subgroup of this group? Otherwise, I don't see why it couldn't have larger symmetry group (e.g. Hopf link has a T^2 subgroup of its symmetry group in S^3). – Ian Agol Mar 18 '12 at 12:29
  • I edited to clarify these points. Thanks! – Jason Cantarella Mar 18 '12 at 13:43

2 Answers2

19

I think there is a non-hyperbolic link that does the job.

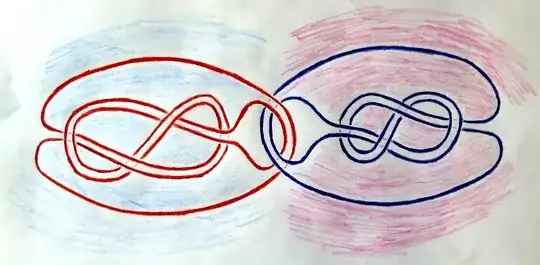
The link that I'm thinking of could be called the splice of two Bing doubles of a figure-8 knot. Another way to describe this link is to start with this 4-component link: Thistlethwaite's link and splice two figure-8 knots against it. You'd splice the knots against the red and purple components, respectively.

above image taken from Morwen Thistlethwaite's homepage. Below is a picture of the link I'm referring to:

enter image description here

The JSJ-decomposition of the complement of this link has 3 incompressible tori, separating the link complement into two Borromean ring complements, and two figure-8 knot complements. There is an orientation-reversing diffeomorphism of $S^3$ that preserves the link, since the Borromean rings admit one, and the figure-8 complements do, too.

As you can see from the way I've drawn it, there is a symmetry that permutes the two components, preserving the orientation of $S^3$, and from the Thistlethwaite diagram you can see a symmetry that reverses the orientation of either component, also preserving the orientation of $S^3$ -- this needs that the figure-8 knot is invertible.

Community
  • 1
Ryan Budney
  • 43,013
5

This is more a comment on Ryan's nice answer than an independent answer itself, but it's too long for a comment box.

Let $K$ be an oriented knot in the solid torus which is isotopic (in the solid torus) to its reverse. [Edit: It should also be amphichiral, as well as invariant under the map of the solid torus which reverses the $S^1$ factor.] Let $L$ be a two component unoriented framed link in $S^3$ which is isotopic to its mirror image (without exchanging the two components) and also has an isotopy which exchanges the two components. Then replacing each component of $L$ with a copy of $K$ yields a two component oriented link in $S^3$ which has the full order 16 symmetry mentioned in the question.

In Ryan's example, $K$ is what I would call a Whitehead double with a funky figure-8 clasp, and $L$ is the Hopf link.

It's relatively easy to think of $K$ and $L$ satisfying the above conditions, so one can construct a large family of examples this way.

Kevin Walker
  • 12,330
  • Thank you for the helpful comments! I thought of something like this, but I didn't think it was easy to come up with K satisfying those three conditions in the solid torus. I completely believe that this will work if you can come up with such a K, but a question for both you and Ryan is this: how do you come up with (families of) such K? – Jason Cantarella Mar 19 '12 at 14:25
  • @JasonCantarella: Coming up with families of knots and links with specified symmetries (and perhaps with additional constraints, like demanding some kind of Brunnian condition) is generally a hard problem. Since hyperbolic 3-manifolds can have any symmetry group, from the perspective of geometrization this becomes the question of which hyperbolic 3-manifolds embed in the 3-sphere. This is a topic of some of my papers. In another direction, Kawauchi has a technique to generate links with prescribe symmetry types (his "Imitation theory") but the symmetry types are fairly restricted. – Ryan Budney Mar 09 '15 at 17:49