Cubic graphs without a perfect matching and a vertex incident to three bridges

Question

The example shown below (courtesy of David Eppstein) is a common example of a cubic graph that admits no perfect matching:

_{(source: uci.edu)}

Are there other examples of cubic graphs that do not admit a perfect matching and, unlike the above example, do not contain a vertex that lies at the intersection of three bridges (i.e. an edge whose removal increases the number of connected components in the graph)?

Incidentally, the 16-vertex graph in the picture above has the smallest number of vertices among all cubic, edge-1-connected graphs without a perfect matching. A proof for this statement was published in Gary Chartrand, Donald L. Goldsmith, Seymour Schuster: A sufficient condition for graphs with 1-factors. Colloquium Mathematicum. Volume XLI, Fascicle 2, 1979. See Corollary 2a on p. 343 for the statement, and p. 341 for a picture. — Peter Heinig, Sep 20 '17 at 15:32

Gjergji Zaimi · Accepted Answer · 2012-06-01T05:02:20.780

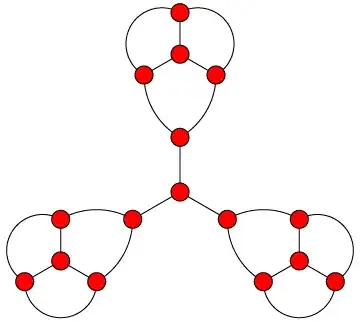
Substitute your central vertex in your graph with a 3-cycle $abc$ so that the graph stays cubic. Now subdivide each edge in this 3-cycle. So we have new vertices $u$ connected to $a$ and $b$, $v$ connected to $b$ and $c$, $w$ connected to $c$ and $a$. Now add a final vertex $x$ and connect it to $u,v$ and $w$. This graph has exactly three bridges, none of which intersect the other at a vertex, and moreover has no perfect matching!

One result which relates the existence of a perfect matching in a cubic graph and its bridges is the following theorem of Petersen from "Die theorie der regularen graphen", Acta Math. 15 (1891), 163-220:

Theorem: Every cubic graph with at most two bridges contains a perfect matching.

As well as this strengthening by Errera, "Du colorage des cartes", Mathesis 36 (1922), 56-60:

Theorem: If all the bridges of a connected cubic graph $G$ lie on a single path of $G$, then $G$ has a perfect matching.

So your instinct is true, in the sense that if the graph has no perfect matching, its bridges do not lie on a path. However the example in the beginning of this answer shows that they are not necessarily incident at the same vertex.

Any two bridges lie on a path, so the second theorem is a strengthening of the first, not a converse. — Brendan McKay, Jun 01 '12 at 03:53

score -1 · Answer 2 · answered May 30 '12 at 15:23

-1

I think there are no such graphs.

It was shown by Sumner and Las Vergnas (you can find the references here: http://mathsci.kaist.ac.kr/~sangil/pdf/2009claw.pdf) that a claw-free connected graph has a perfect matching (assuming even number of vertices, of course!). An intersection of three bridges is clearly a claw.

answered May 30 '12 at 15:23

Felix Goldberg

6,872

1

@Felix: What you are saying is that: no perfect matching implies there is a claw. But a claw does not necessarily imply three bridges. So this does not address the question. – Gjergji Zaimi May 30 '12 at 15:30
This is surely simple, but given that every vertex in a cubic graph has by definition three neighbours, how can any cubic graph be claw-free? – Anthony Labarre May 30 '12 at 15:32
@Anthony, pick your favourite cubic graph and substitute each vertex with a triangle. You get a claw free cubic graph. – Gjergji Zaimi May 30 '12 at 15:33
@Gjergji Zaimi: Oh, right, I had overlooked the induced subgraph part ;-) Thanks! – Anthony Labarre May 30 '12 at 15:38
Sorry for the wrong answer... – Felix Goldberg Jun 01 '12 at 10:20

Cubic graphs without a perfect matching and a vertex incident to three bridges

2 Answers2

Linked