3

1) The field outside a solenoid is approximated to be zero, because of opposites points "cancelling out". Does this approximation of the field being almost zero become worse as the diameter of the solenoid increases? (since the opposite sides are further apart) I'm looking for an answer for two cases: 1) Only the diameter increases, but all other dimensions remain the same. 2) All dimensions increase proportionally, keeping the aspect ratio the same.

2) Are solenoids approximated as a series of perfect circles (since opposite sides cancel only in a circle)? And consequently shouldn't a stretched out solenoid's field be completely different since its nothing like a series of circles?

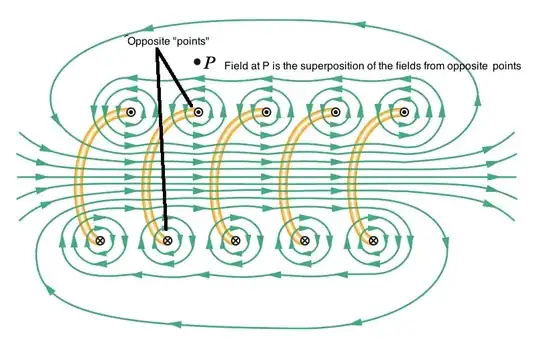
EDIT: enter image description here

The field at P is the superposition of the fields from the opposite "points". If the diameter of the solenoid increases, the bottom "points" are further away from $P$, so their contribution to the field decreases. Therefore the assumption that the fields from the top points cancel with the bottom points becomes falser/less valid.

dfg
  • 2,009
  • 1
    Related: http://physics.stackexchange.com/q/70452/ – Tobias Mar 06 '14 at 17:31
  • One reason the current answers do not contain enough detail is because the question is not clear enough. You should specify exactly what you mean by "the diameter of the solenoid increases". What happens to the other distances? It matters because it affects the answer, or even whether the question makes sense. A better way to get better answers is to spend time improving the question, on top of spending reputation. – Emilio Pisanty Mar 10 '14 at 22:41

1 Answers1

2

Mostly, yes on both counts.

  1. It depends whether the solenoid also gets longer as it gets wider. The approximation that the field outside the solenoid vanishes is valid for points whose distance to the solenoid's centre is much smaller than the distance to both ends. This is impossible for a point outside a solenoid that's wider than it is tall.

    To answer your more specific question about opposite points, the reason these points still cancel is because there is more current per unit angle as the solenoid gets wider if the distance remains fixed. It's more complicated than this - the field really vanishes because of the cancellation of the complete integral over the infinite surface - but one good picture to keep in mind is the following.

    enter image description here

  2. The field of a solenoid that's considerably stretched, or of a series of circles that are widely separated, is indeed different to that of an 'ideal' solenoid, which is usually modelled as a surface current, with no interruptions, over a cylinder. For a real solenoid with spacings between the loop, the approximation will hold for points whose distance to the nearest point on the solenoid is greater than the inter-loop spacings.

Emilio Pisanty
  • 132,859
  • 33
  • 351
  • 666
  • Sorry, I don't understand the first part of your answer. Why would the width increasing affect the validity of the approximation? The field above two opposing points is the superposition of the field of both points. Increasing the distance would increase the difference in fields from the opposing points worsening the superposition approximation of zero. How would adding more "opposite points" (a consequence of increasing the width) result in a better approximation? – dfg Mar 06 '14 at 17:23
  • "The field above two opposing points is the superposition of the field of both points". What two points are you thinking of? In general, the field is a superposition of the field generated by all of the solenoid, regardless of where you are. – Emilio Pisanty Mar 06 '14 at 17:45
  • 1
    Also, to be clear, increasing the width without maintaining the aspect ratio will in general tend to degrade the approximation, not make it better. – Emilio Pisanty Mar 06 '14 at 17:46
  • 2
    All true. Mind you, in my solenoid lab I give one of the groups a coil of 11 turns in 9 cm and they still get results within about 5% of the ideal value for the interior field and less that 1/10 of the interior field "near" the side of the coil on the outside. (This is a exercise where they measure the current dependence of field in their device and share their data with the class to measure the dependence on the turn-density, so they get to see a "good" example too.) – dmckee --- ex-moderator kitten Mar 07 '14 at 02:57
  • @EmilioPisanty I added in a diagram and an explanation to better explain what I mean by my first question. – dfg Mar 10 '14 at 00:17
  • @dfg then my comment above holds. It is not the cancelling out of the fields from those two 'opposite' points that makes the field outside vanish, it is the contributions from the entire solenoid. – Emilio Pisanty Mar 10 '14 at 00:25
  • Right, but all the contributions can be expressed as the sum of the superposition of the all the two "opposite points", right? And if the difference between field contributions from the opposite points increases doesn't the entire sum increase too? – dfg Mar 10 '14 at 00:34
  • As I said, it depends on whether the aspect ratio is kept fixed. If the length is fixed, then yes, you are correct. If the aspect ratio is kept fixed then there are extra terms that go into the sum that make up for the differences. – Emilio Pisanty Mar 10 '14 at 10:13
  • I'm sorry, but I still don't follow. You want the sum to be as close to zero as possible. Your'e saying keeping the aspect ratio fixed improves the approximation because extra terms are added to the sum. But adding extra terms to the sum only increases it, which makes the approximation worse (since the total sum is made even larger). – dfg Mar 10 '14 at 17:02
  • It's not possible to go into that much depth unless you specify exactly how the solenoid's width increases. (Is the length constant, or proportional to the width? Is the point's distance to the axis fixed? Is its distance to the surface fixed? Or proportional to the width?) – Emilio Pisanty Mar 10 '14 at 17:30
  • On the other hand, I did miss an important part of the argument, which I've edited in. – Emilio Pisanty Mar 10 '14 at 17:41
  • I'm considering two cases - one where the width remains the same and one where it increases, maintaining the aspect ratio. The point's distance to the surface is fixed. – dfg Mar 11 '14 at 14:02
  • Sorry, I don't see how increasing the current per unit angle reduces the sum. – dfg Mar 12 '14 at 16:11
  • Help please? I'd be glad to give you the bounty if you help me out. – dfg Mar 13 '14 at 13:26
  • Well, do you see how increasing the current per unit angle increases the contribution of that part? How do you think that compares to the decrease in that contribution due to the increased distance? – Emilio Pisanty Mar 13 '14 at 16:35