As the Feynman diagram shows above. Does the $s$-channel and $t$-channel stands for exactly same reaction or they have big difference?
Asked
Active
Viewed 2.1k times
20
-
4The nature of the limits on the two channels imposes very strong limits on the reactions that you can chose if you want to diagram both channels for a single reaction. It is those combined limits that are responsible for the apparent similarity of the two diagrams. By contrast $e^+ + e^- \to \mu^+ + \mu^-$ can only proceed by your left-hand diagram and $e^- + \mu^- \to e^- + \mu^-$ can only proceed by the right-hand diagram. – dmckee --- ex-moderator kitten May 16 '14 at 04:37
-
in addition to the limits of quantum numbers, the kinematics of the interaction can be a significant factor. For example, substitute the gamma with the Z boson in your interactions (which is indeed relevant in case of high energies). Then if the collision happens at energy of about Z boson mass, i.e. sqrt(s) ~= m(Z), the s-channel dominates. But depending on the kinematic phase space of the interaction, you might have a situation where the t-channel is dominant. These two cases correspond to the answer by @JamalS: M ~= 1/(s-m^2) @ s~=m^2 VS M ~= 1/(t-m^2) @ t~=m^2. – xealits Feb 25 '20 at 17:52
-
related: https://physics.stackexchange.com/q/330717/226902 https://physics.stackexchange.com/q/340077/226902 https://physics.stackexchange.com/q/110112/226902 – Quillo Jan 11 '23 at 18:00
3 Answers
16
To every Feynman diagram we associate a set of integrals which compute the corresponding scattering amplitude according to the Feynman rules. An example of such an amplitude:
$$\mathcal{M}=(-ig)^2\left[ \frac{i}{(p_1-p'_1)^2-m^2}+\frac{i}{(p_1+p_2)^2-m^2}\right]$$
from a tree-level process in scalar Yukawa theory. In the case of two-body to two-body scattering, we denote the incoming momenta as $p_1,p_2$ and the outgoing as $p'_1,p'_2$. We introduce Mandelstam variables which arise commonly in amplitudes:
$$s=(p_1+p_2)^2=(p'_1+p'_2)^2$$ $$t=(p_1-p'_1)^2=(p_2-p'_2)^2$$ $$u=(p_1-p'_2)^2=(p_2-p'_1)^2$$
Our amplitude corresponded to a set of Feynman diagrams:
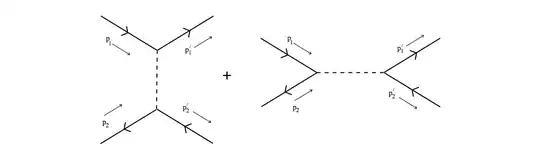
If we substitute for our Mandelstam variables, we see the first diagram has $\mathcal{M}\sim 1/t$ and the second diagram $\mathcal{M}\sim 1/s$. Hence we say the first involves a t-channel and the other an s-channel. The $s$ measures the total centre of mass energy of the collision, whilst $t,u$ are measures of momentum exchanged between the particles.
JamalS
- 19,254
-
1This is a time when I'd love to hear more, if you have more to say? I've never truly gotten my head around this and QFT interaction amplitudes in general myself, but this has certainly been a help. I know you've got a big long technical answer in you! :) It took me several minutes to figure out why, but dmckee 's comment is also very enlightening. Thank you. – Flint72 May 16 '14 at 13:56
-
@Flint72: What do you mean by saying you haven't gotten your head around QFT scattering amplitudes? Do you mean conceptually, or you can't compute them? – JamalS May 16 '14 at 14:44
-
A little bit of both. I can compute some of them, but a lot of it is memory work, as opposed to 'knowing whats going on'. So if I were to come across a new one, it would take an awful lot of fustration and mastakes and staring blank at the page to figure it out. This has been the case with lots of types of calculations over the years, and usually, eventually, after doing them enough times and thinking about them enough it all makes sense and you can do a new one right off the bat. I am nowhere near there with QFT however! – Flint72 May 16 '14 at 15:02
-
@Flint72: As you have many issues with QFT, I can only direct you to resources - I can't address them all in a single answer. – JamalS May 16 '14 at 15:04
-
Oh, sorry, I didn't expect you to try to 'teach me to calucalute in QFT' in one go, something that would take a good supervisor much hard work! It would be a very tall order indeed! Rather, I was just saying in general, that you explain it well. I guess I should search through for other QFT calculation related answers that you have online. My apologies for the confusion. – Flint72 May 16 '14 at 15:13
6
They are related by Crossing symmetry, see e.g. here, which is a fundamental property of scattering amplitudes valid to all orders and even beyond QFT.
TwoBs
- 5,004
-
Why is this downvoted? I do not konw the answer myself, but I am wondering what is wrong with this? Is it just the last clasue perhaps? I was lead to believe that Crossing Symmetry is a real thing? – Flint72 May 16 '14 at 13:56
-
Indeed, why my answer was downvoted when it is, in fact, the only one that contains the right words "crossing symmetry?" – TwoBs May 16 '14 at 17:44
4
They represent the same reaction, electron-positron scattering in the two possible ways it can happen to first order.
Feynman diagrams are a pictorial representation of the integrals that have to be added in the perturbative series expansion of the theoretical formula for the scattering cross-section. Like any expansion, there are constants term multiplying each order that determines the contribution of each order which diminishes as the order gets higher. Look at this Taylor series. For perturbative expansions these are the coupling constants, and the terms entering are counted as, first order, second order, etc. In your diagrams, the electromagnetic coupling constant or ~1/137 ensures that the higher terms can be ignored.
The two diagrams are the first order contributions to the cross-section and have to be both taken into account in order to calculate and predict the cross section for the process to first order in the coupling constants involved in the interaction.
