Kinetic theory derivation of viscosity of a gas

Question

Encountering a lot of issues trying to understand this. The basic idea of the derivation I'm using is as follows (the image here may help):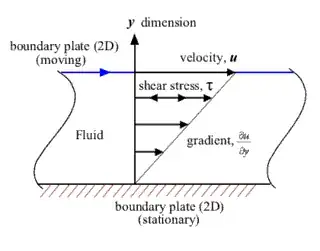
_{(source: tamu.edu)}

I'm going to write $\langle u_x\rangle$ as the general horizontal speed instead of $u$ and save $u$ as the horizontal speed of the top plate.

So the idea is that we have our gas between two plates, the top one moving at constant speed $u$ and the bottom one fixed. Now this apparently means that we should get a transport of momentum through the gas, from the top plate down towards the bottom plate. However, how can this be? If you look at the gas as a whole, it is in a steady state, in that each layer is moving at a constant speed due to whatever velocity gradient $$\frac{d\langle u_x\rangle}{dy}$$ exists. Therefore, how is momentum being transported throughout the gas - if this were the case, surely layers would be changing their horizontal speeds and so we wouldn't have this steady state.

Then the shear stress from the force needed to keep the top plate moving is $$\frac{F}A$$ and this is used to define the viscosity $$\eta$$ via $$\frac{F}A=\eta\frac{d\langle u_x\rangle}{dy}.$$ This also applies to any 'layer' of the gas, with $F$ the force needed to keep it moving at constant speed.

The next step is to note that $$-\frac{F}A$$ is the momentum flux of the gas molecules through unit area of a layer of the gas. I don't understand this at all. So we have a layer of gas, and we're dragging it along at constant speed $$\langle u_x\rangle$$ by applying some force $$F.$$ Using force as the rate of change of momentum, I accept that $$\frac{F}A$$ represents the change in momentum in unit time of unit area of this layer, along the x direction. However how does this equal the x direction momentum of the molecules that passes through unit area in unit time of this layer? They seem to be unrelated.

Finally to calculate this flux (allowing us to find $$\eta$$) we use the fact that the number of particles in the speed interval $$[v,v+dv]$$ and the angle interval $$[\theta,\theta+d\theta]$$ is given by $$\frac{1}2nvf(v)\cos\theta \sin\theta\; dv\;d\theta$$. Then we say each molecule has travelled one mean free path $$\lambda$$ since it's last collision and so a distance $$\lambda \cos\theta$$ along the $$y$$ direction. This corresponds to a speed difference $$d\langle v_x\rangle=\frac{dv_x}{dy}dy=\frac{dv_x}{dy}\lambda \cos\theta$$ and so the momentum from this source is larger than that in our layer by an amount $$-m\left(\frac{d\langle u_x\rangle}{dy}\right)\lambda \cos\theta.$$ This is then multiplied by the above distribution and integrated over all speeds and all angles $$v\in[0,\infty]\qquad\text{and}\qquad\theta\in[0,\pi].$$ My issue with this bit is, why don't we just find the total momentum rather than the amount by which it exceeds the momentum of that layer?

This gives us the flux, so the shear stress, so by comparison $$\eta.$$ If anyone could give me some insight on at least one of those things I would be very grateful.

Answer 1

how is momentum being transported throughout the gas - if this were the case, surely layers would be changing their horizontal speeds and so we wouldn't have this steady state.

The gas is in a steady state, and momentum is being transferred. This means that a steady horizontal force on the top plate is required, and an equal and opposite force on the bottom plate. Each layer of gas receives momentum from above, and transfers the same momentum to the layer below it, so it undergoes no acceleration.

$F/A$ represents the change in momentum in unit time of unit area of this layer

The layer has a steady speed, so it has no change in momentum per unit time. $F/A$ is the momentum transferred from one layer to the one below it.

However how does this equal the x direction momentum of the molecules that passes through unit area in unit time of this layer? They seem to be unrelated.

At the microscopic level, the only way one layer can impart momentum to the adjacent layer is by swapping molecules. $F/A$ is the net momentum carried across the imaginary boundary from the upper to the lower layer.

why don't we just find the total momentum rather than the amount by which it exceeds the momentum of that layer?

$F/A$ is the net momentum carried across the imaginary boundary. For every molecule passing downwards through the boundary, there is on average a molecule passing upwards, carrying on average slightly less $x$ momentum, characteristic of the region it came from.

As you can see (I hope), the derivation was correct - all I have done is tweak the words. There is often a tendency in textbooks to assume that if a quantity obviously has the correct dimensions, then it must be what is wanted. This can lead to a casual use of words when describing the logic. hth

I notice that you also have solid plates at the top and bottom of your diagram, which require that you use the no-slip boundary condition. This is always good when the mean free path is small, but for an accurate result for arbitrary mean free path you would need to know something about the surface, and how it interacts with incident molecules.