What is the relationship between entropy and work?

Question

Can someone explain the relationship between entropy and work? I've been reading my textbook and looking online but I feel like I'm missing something. Can someone explain it in layman's terms :)

Answer 1

Let's frame this question in terms of a heat engine (Carnot engine).

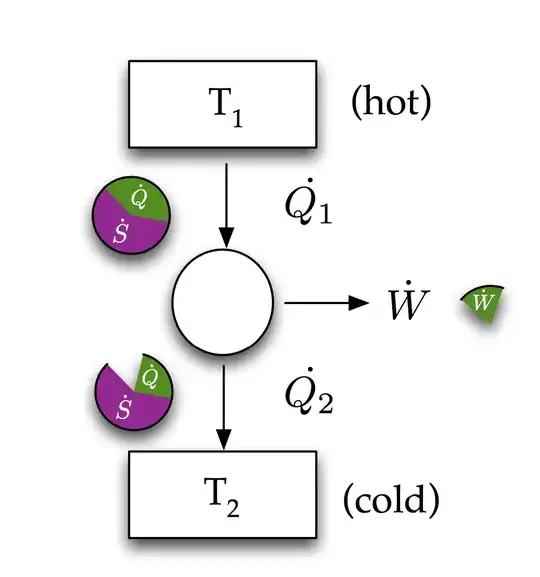
Here is a diagram I made for a class when teaching this stuff.

Heat flow $\dot{Q}$ has an associated entropy flow $\dot{Q}/T$. The job of a thermodynamic engine is extract/filter as much useful work as possible from a flow of energy and entropy.

To answer your question in layman terms. Work is entropy free energy, it is what you have managed to extract/filter from a flow of heat by rejecting entropy. In this context entropy is a measure of inaccessible energy (i.e. a part of heat flow that cannot do work).

Answer 2

Introduction: Entropy Defined

The popular literature is littered with articles, papers, books, and various & sundry other sources, filled to overflowing with prosaic explanations of entropy. But it should be remembered that entropy, an idea born from classical thermodynamics, is a quantitative entity, and not a qualitative one. That means that entropy is not something that is fundamentally intuitive, but something that is fundamentally defined via an equation, via mathematics applied to physics. Remember in your various travails, that entropy is what the equations define it to be. There is no such thing as an "entropy", without an equation that defines it.

Entropy was born as a state variable in classical thermodynamics. But the advent of statistical mechanics in the late 1800's created a new look for entropy. It did not take long for Claude Shannon to borrow the Boltzmann-Gibbs formulation of entropy, for use in his own work, inventing much of what we now call information theory. My goal here is to shwo how entropy works, in all of these cases, not as some fuzzy, ill-defined concept, but rather as a clearly defined, mathematical & physical quantity, with well understood applications.

Entropy and Classical Thermodynamics

Classical thermodynamics developed during the 19th century, its primary architects being Sadi Carnot, Rudolph Clausius, Benoit Claperyon, James Clerk Maxwell, and William Thomson (Lord Kelvin). But it was Clausius who first explicitly advanced the idea of entropy (On Different Forms of the Fundamental Equations of the Mechanical Theory of Heat, 1865; The Mechanical Theory of Heat, 1867). The concept was expanded upon by Maxwell (Theory of Heat, Longmans, Green & Co. 1888; Dover reprint, 2001). The specific definition, which comes from Clausius, is as shown in equation 1 below.

S = Q/T

Equation 1 In equation 1, S is the entropy, Q is the heat content of the system, and T is the temperature of the system. At this time, the idea of a gas being made up of tiny molecules, and temperature representing their average kinetic energy, had not yet appeared. Carnot & Clausius thought of heat as a kind of fluid, a conserved quantity that moved from one system to the other. It was Thomson who seems to have been the first to explicity recognize that this could not be the case, because it was inconsistent with the manner in which mechanical work could be converted into heat. Later in the 19th century, the molecular theory became predominant, mostly due to Maxwell, Thomson and Ludwig Boltzmann, but we will cover that story later. Suffice for now to point out that what they called heat content, we would now more commonly call the internal heat energy.

The temperature of the system is an explicit part of this classical definition of entropy, and a system can only have "a" temperature (as opposed to several simultaneous temperatures) if it is in thermodynamic equilibrium. So, entropy in classical thermodynamics is defined only for systems which are in thermodynamic equilibrium.

As long as the temperature is therefore a constant, it's a simple enough exercise to differentiate equation 1, and arrive at equation 2.

$\Delta$S = $\Delta$Q/T

Equation 2 Here the symbol "" is a representation of a finite increment, so that S indicates a "change" or "increment" in S, as in S = S1 - S2, where S1 and S2 are the entropies of two different equilibrium states, and likewise Q. If Q is positive, then so is S, so if the internal heat energy goes up, while the temperature remains fixed, then the entropy S goes up. And, if the internal heat energy Q goes down (Q is a negative number), then the entropy will go down too.

Clausius and the others, especially Carnot, were much interested in the ability to convert mechanical work into heat energy, and vice versa. This idea can lead us to an alternate form for equation 2, that will be useful later on. Suppose you pump energy, U, into a system, what happens? Part of the energy goes into the internal heat content, Q, making Q a positive quantity, but not all of it. Some of that energy could easily be expressed as an amount of mechanical work done by the system (W, such as a hot gas pushing against a piston in a car engine). So that Q = U - W, where U is the energy input to the system, and W is the part of that energy that goes into doing work. The difference between them is the amount of energy that does not participate in the work, and goes into the heat resevoir as Q. So a simple substitution allows equation 2 to be re-written as equation 3.

S = (U - W)/T

Equation 3 This alternate form of the equation works for heat taken out of a system (U is negative) or work done on a system (W is negative), just as well. So now we have a better idea of the classical relation between work, energy and entropy. Before we go on to the more advanced topic of statistical mechanics, we will take a useful moment to apply this to classical chemistry.

Read more:http://www.tim-thompson.com/entropy1.html

Answer 3

Entropy is fundamentally a subjective quantity, it is the amount of information needed to specify the exact physical state of a system given it's macroscopic specification. The fact that you don't know the exact physical state of a system, yet the laws of physics are such that information is never lost, implies the second law of thermodynamics (one also needs to assume low entropy initial conditions for the universe).

If given the macroscopic specification of an isolated system there are $N$ possible physical states it could be in, then changing some external parameter like the volume, cannot possibly lead to a new macroscopic specification that is consistent with less than $N$ physical states. If this were possible then the time evolution of the system would necessarily be such that two or more different initial states would evolve to the same final state. Information about the initial state would thus be lost, which would violate fundamental laws of physics.

To specify the number $N$ you need to specify the string of its binary digits, such a string will have a length of $\log_2(N)$, so the entropy is proportional to the logarithm of of the number of possible physical states. Now, as I explained above it is clear that the entropy of an isolated system can never decrease, but it also seems to imply that it cannot increase either. So, how come the entropy of isolated system does actually increase in case of so-called irreversible changes? Let's consider the example of free expansion. We have some gas that fills half of a container and we remove the separation between the two parts. To be completely rigorous here we consider the hypothetical case of a completely isolated system such that not even quantum decoherence due to interactions with the environment takes place. While completely unrealistic, physically the absence of extremely weak interactions cannot possibly make any difference for down to Earth thermodynamics.

So, the gas could initially have been in one of some number $N$ of physically distinct states, and the outcome of the free expansion in a completely isolated system is described by a one to one mapping from initial to final states that maps each of these $N$ initial states to some final state, so you have $N$ possible final states. However, while there are indeed only $N$ states the gas can really be in, there are a vastly larger number of states that have macroscopic properties that look exactly like any of these $N$ states. So, given only the macroscopic properties of the final state, there are far more physical states compatible with it than only the $N$ states from which the gas could have ended up in after the free expansion.

The fact that the real number of physical states is less due to its history of having undergone free expansion is not something that can be utilized using only macroscopically available means. If you could let the system evolve back in time, then the distinction would matter. It would then look like if the entropy decreases, but that's an artifact of the subjective increase of the entropy due to the ignorance about the real physical state having grown larger due to there being more physical states that look exactly like the same like the physical states it can really be in.

A simple analogy: Suppose you have made counterfeit money which is so perfect that you cannot distinguish it from real money, but with very sophisticated methods it can be distinguished, but only the police has access to such methods. If you then make the stupid mistake of mixing up your real money with your counterfeit money, then you have lost the information about what money is real and what is counterfeit. So, while the information is actually still there physically, it's not accessible to you, given how the money looks to you, you cannot tell if it is real or counterfeit. For you this has real consequences, it imposes real constraints on how you can operate. The case of entropy increase is similar, while purely subjective, it still imposes constraints on what we can do in practice.

So, how doe this all relate to the amount of work we can let a system perform? letting a system perform work amounts to extracting energy from it and putting that energy in just a few degrees of freedom. E.g. if we use the expansion of a gas to lift a weight, then we extract internal energy from the gas which goes into the potential energy of the weight. To specify the state of the system comprising of the gas plus the weight one needs to specify the state of the gas plus just one degree of freedom, the height of the weight.

Now, the less energy an isolated system has, the less physical states will be available for it, so extracting work from an isolated system in thermal equilibrium is impossible. If the system was not in equilibrium, like in case of the initial state of the gas about to undergo free expansion, then one ca extract work from it. Since the number of possible states is going to increase, you can extract so much energy from it such that the final macro state will be compatible with the same number of states it was compatible with it in the initial state.

Then, one can still ask if the subjective nature of entropy could in theory allow one to extract more work from a system than is allowed under standard thermodynamics. To see how this is possible, one can consider the so-called Laplace's Demon though experiment, which is a variant of the Maxwell Demon thought experiment. In the maxwell's Demon though experiment one considers a gas in a container with a separation. The gas in the two parts are initially in mutual thermal equilibrium. The Demon can open a small door in the separation and then molecules from one part can enter into the other part. One can consider the Demon letting through fast molecules from part 1 to part 2 and onl slow molecules from part 2 to part 1. By doing that a temperature difference is created, the entropy seems to go down, which means that work can be extracted from the system after the Demon has acted on it.

The solution to this paradox comes from recognizing that the Demon doesn't have any information about when to open or close the door, it has to acquire that information from the state of the gas. The information it acquires changes its physical state, to be able to operate on the long term it has to return to the same physical state. As I pointed out earlier, you cannot let an isolated system erase information different possible physical states cannot evolve to the same physical state, at most the Demon can dump the information somewhere else so that it can itself return to the same physical state. That then has the net effect of the information that was present in the gas from ending up to the Demon and then from the Demon it ends up somewhere else. The entropy decrease of the gas then leads to the entropy of some other system to increase.

But what if the Demon could calculate the state of the gas in advance? Suppose that the state of the gas while looking very chaotic can actually be predicted by a simple algorithm? So, the Demon just runs a simple algorithm to decide whether or not to close the door, the gas one one side cools the other sides heats up, work can be extracted so it seems that the entropy is now really lowered without there being some hidden entropy costs. In this case, this is indeed happens. There is then a difference between the initial entropy being attributed to the number of states with the same macroscopic properties and the fact that the gas actually is in one out of a far smaller number of states that it can be in according to the algorithm that the Demon has access to.

So, you could then say that the entropy was actually never as high as we thought it was, but that actually misses the fundamental point that entropy is always a subjective quantity. If you have complete knowledge about the exact physical state, then with only one physical state the system can be in (the one it actually is in), the entropy would be zero.