In particle physics, the mathematical framework that is currently used is known as quantum field theory. An example of such a theory is quantum electrodynamics, which deals with the interactions between photons and electrons.
When doing calculations in quantum field theory, you find yourself dealing with a lot of (some times very complex) formulas. Feynman found a way to nicely represent this formulas as diagrams. Two examples of Feynman diagrams are:
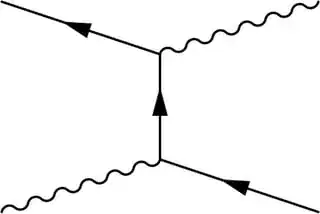

If you are studying a physical process and you want to make predictions about it there's a recipe to do your calculations:
Draw all the Feynman diagrams corresponding to the process in question. Each diagram has an associated mathematical formula. By adding all of them one gets the physical answer.
There are also some rules (known as Feynman rules) that are used draw diagrams. In general, what you have to do is:
For each incoming photon draw a wavy line on the left, for each incoming electron or positron a solid line (the arrow towards the left means a positron and towards the right an electron) and the same for outgoing particles. Then use the Feynman rules to construct an allowed diagram.
We could stop here. Feynman diagrams are just a nice way of representing some complicated formulas. We know how to use them to get experimentally testable answers to questions about the physics of electrons and photons. The results that can be obtained in this way describe nature impressively precisely (as is the case of the Lamb shift, some effect in the hydrogen atom).
However, because every incoming and outgoing line represents a particle, it is tempting to say that the internal lines of the diagram are also particles. Physicist sometimes call them virtual particles, but the concept of virtual particle has very little to do with the one of particle. Notice that a Feynman diagram doesn't even describe a physical process. It's just a way of representing some mathematical formula.
Why do physicist use that name, then? The answer is that when talking about calculations in quantum field theory, it can be used as a useful metaphor. You can talk about diagrams in a natural way as if they were physical processes with time represented as flowing from left to right and with particles colliding, being created, destroyed, etc.
In this metaphor, virtual particles can travel faster than the speed of light, for example. Nevertheless, when you translate this metaphoric language into the actual formulas and add them for all the diagrams, the results are agree with special relativity. The real particles never get to go faster than light.
In the first of the example diagrams above, the internal vertices can be moved so that one is on the left of the other, so in our metaphor one occur before the other. Then we can move them again and make the one that was in the left be now in the right. The internal solid line representing an electron would then change from going forward in time to going backwards. The metaphor plays nicely with this and allows us to see the electron going backwards as a positron (as both are represented by a solid line with an arrow to the left). Again, none of this is real, it is just a nice way of talking about some calculations.
In the second diagram, you can see an example of virtual creation and annihilation of an electron-positron pair from and to a photon. This is just a fancy way of talking about one diagram in the set of the Feynman diagrams describing the propagation of a photon.
So, to summarize and be very clear:
In quantum field theory special relativity is not violated, and it is impossible for any particle (in particular, electrons) to go faster than the speed of light or backward in time.

