0

I was watching a Brian Cox lecture, and he touched upon the notion that if two objects were moving towards eachother at the speed of light and collided, they would collide at no greater than the speed of light, when they should collide at twice the speed of light I believe. Why is this?

Qmechanic
  • 201,751
Charlie
  • 271
  • 4
    http://hyperphysics.phy-astr.gsu.edu/hbase/Relativ/einvel2.html. The observed velocity is u' = (c+c)/(1+c^2/c^2) = 2c/2 = c – NoethersOneRing Apr 13 '17 at 17:23
  • Why does this happen? – Charlie Apr 13 '17 at 18:26
  • According to the theory of special relativity, the two frames of reference have different clock rates and measured distances , and the notion of simultaneity in the direction of motion is altered, so the addition law for velocities is changed –  Apr 13 '17 at 19:03
  • Related: http://physics.stackexchange.com/q/11398/2451 and links therein. – Qmechanic Apr 13 '17 at 22:13
  • @WillyBillyWilliams, neither object has an inertial reference frame (IRF) since both have speed $c$ in any IRF. – Hal Hollis Jun 12 '17 at 16:14
  • @NoethersOneRing, one of the velocities in the numerator of the relativistic velocity addition formula must be less than $c$ since one of the terms is the relative velocity $v$ of the two inertial reference frames and $v \lt c$. – Hal Hollis Jun 12 '17 at 16:36
  • @NoethersOneRing of course, but you can still imagine the limit v->c –  Jun 12 '17 at 21:08

1 Answers1

0

(This answer elaborates on the comment from @Armando .)

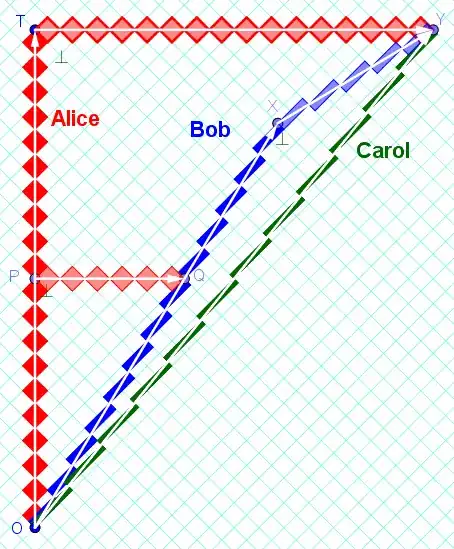
Consider this spacetime diagram on rotated graph paper.

Velocity Composition spacetime diagram on rotated graph paper

Alice uses Minkowski-right triangle OPQ, with right-angle P and legs parallel to her axes to declare that Bob has velocity $v_{BA}=6/10$ with respect to Alice. (Any triangle similar to OPQ could be used to determine this velocity.)

Bob uses Minkowski-right triangle OXY, with right-angle X and legs parallel to his axes to declare that Carol has velocity $v_{CB}=5/13$ with respect to Bob.

So, what is the velocity of Carol with respect to Alice?
Alice uses Minkowski-right triangle OTY, with right-angle T and legs parallel to her axes to declare that Carol has velocity $v_{CA}=16/20$ with respect to Alice.

These velocities are related by the velocity composition formula $$\begin{align}v_{CA} &=\frac{v_{CB}+v_{BA}}{1+v_{CB}v_{BA}}\\ &=\frac{(\frac{5}{13})+(\frac{6}{10})}{1+(\frac{5}{13})(\frac{6}{10})}=(\frac{4}{5}) \end{align}$$ (This is the equation used by @NoethersOneRing .)

The Euclidean analogue of this is asking how "slopes" "add [compose]".
Geometrically, angles add... and slopes are equal to the tangent-function of the angle... but slopes don't add.
In special relativity, using the Minkowski-angle [the rapidity $\theta$, where $v=\tanh\theta$ and $\gamma=1/\sqrt{1-v^2}=\cosh\theta$], we have $$\begin{align}v_{CA}=\tanh_{CA} &=\tanh(\theta_{CB}+\theta_{BA})\\ &=\frac{\tanh\theta_{CB}+\tanh\theta_{BA}}{1+\tanh\theta_{CB}\tanh\theta_{BA}}\\ &=\frac{v_{CB}+v_{BA}}{1+v_{CB}v_{BA}}\\ \end{align} $$

So, in this example, (using a calculator or WolframAlpha) $$v_{CA}=\tanh(\rm arctanh(5/13) + arctanh(6/10) )=4/5.$$

For the speed of light case, $$v_{CA}=\tanh(\rm arctanh(1) + arctanh(1) )=1,$$ which implicitly uses $\infty+\infty=\infty$.

[In Galilean relativity, Galilean-angles add and slopes [i.e. velocities] add. Unfortunately, our common-sense has brainwashed us into thinking that velocities always add.]

robphy
  • 11,748