Pulling on Yo-yo so it doesn't rotate

Question

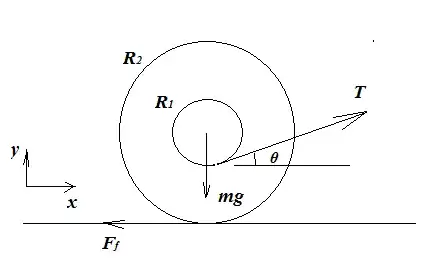
So say we want to find the angle $\theta$ from the horizontal to pull a yo-yo like in the diagram so it doesn't rotate. I have seen a solution where you analyze the torque about the contact point. Since rolling can be viewed as a rotation about the contact point, we want the tension line to go through the contact point so there is no torque. So that would mean we want $\sin(90^{\circ} - \theta) = \frac{R_1}{R_2}$.

However, if I consider the torques about the center of the yo-yo, I get a different answer. The normal force is $F_N = mg - T\sin{\theta}$, so thus the frictional force is $F_{f} = F_N\mu$ if $\mu$ is the coefficient of kinetic friction. Thus we have that if the torque about the center of the yo-yo is zero, we must have $R_1T = R_2F_{f}$, where $F_{f} = (mg - T\sin{\theta})\mu$. However, this does not imply that $\theta = \frac{R_1}{R_2}$. In fact, if we use the fact that you must be moving to the right for there to be any rotation, we get $T \cos{\theta} \geq F_{f}$, and this means that $R_2T\cos{\theta} \geq R_1T$, implying that $\cos{\theta}\geq\frac{R_1}{R_2}$, where equality occurs when $T\cos{\theta} = F_f$, implying there is no horizontal acceleration if it is to agree with the other solution. But this is definitely false, as it is possible for there to be horizontal acceleration. So what's wrong with this solution?

Answer 1

This recent question and its answers are relevant.

Setting the torque about the point of contact with the ground to zero means that you are assuming the angular momentum, $L=m\boldsymbol{r}\times\boldsymbol{v}$, about this point to be constant. In other words, the linear velocity of the yo-yo is assumed to be constant.

In your second case, setting the torque about the centre of mass to zero gives you the condition for no rolling, and this does not say anything about the linear acceleration of the yo-yo.

Also, for a sanity check, consider the result of $\cos(\theta)=R_1/R_2$ supposedly giving an angle, $\theta$, at which you can pull at the yo-yo without it rolling regardless of how hard you pull. This doesn't really make sense if you consider that you can always pull hard enough such that the normal force acting at the contact point vanishes, i.e. $F_N=mg-T\sin\theta=0\implies T=mg/\sin\theta$ will result in zero normal (and hence frictional) force. So it is possible to achieve no-roll motion at any angle to the horizontal.