When we calculate the Hamiltonian in the free theory, we notice that it contains an infinitely large term \begin{align} H &= \int_V \mathrm{d }k^3 \frac{\omega_k}{(2\pi)^3 } a^\dagger(\vec k) a(\vec k)+ \frac{1}{2} \int_V \mathrm{d }k^3 \omega_k \delta(\vec 0) \, . \end{align} We can get rid of this term by claiming that nature only uses normal ordered operators, in which case there is no infinitely large term.
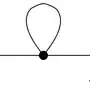
As soon as add an interaction term like $\phi^4$, we encounter the same problem. If we switch the operators around using the commutation relations we find infinitely large terms that are all related to field commutators evaluated at the same spacetime point $[\phi_{-}(x) ,\phi_{+}(x)] \sim \infty $. In diagrammatic form, these terms are given by self-loop diagrams
Again, the problem can be solved by demanding that the Hamiltonian is brought into normal form before we quantize it. If we work with a normal ordered Hamiltonian there are no self-loop diagrams.
This seems to suggest that if we work with normal ordered Hamiltonians, at least some of the vacuum bubble diagrams no longer exist. Does normal ordering remove all vacuum bubble diagrams or are there some remnant diagrams that are not removed through the process of normal ordering?