Axially Symmetric Lens Integration

Question

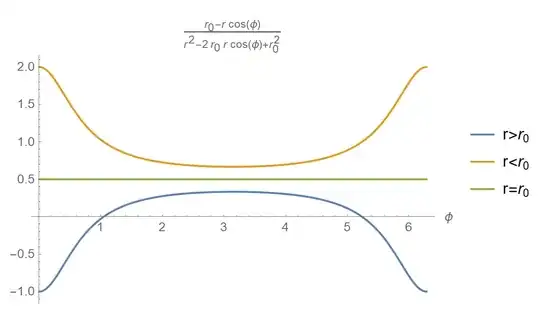
I'm trying to understand the deflection of light due to an axially symmetric gravitational lens following chapter 2.3 of these Heidelberg lecture notes. In doing so, I encounter the integral (2.12 a)

$$\int_0^{2\pi} \frac{r - r'\cos(\phi)}{r^2 + r'^2 - 2rr'\cos(\phi)}\,d\phi$$

which apparently vanishes for $r'>r$ and is $2\pi/r$ for $r'<r$. I've tried to understand how this answer comes about, but to no avail. I couldn't find it in an integral table and I can't get Mathematica to give me a useful answer unless I plug in specific values for $r,r'$.

Answer 1

Let $$I(r_0,r;a,b)=\int_a^{b}\frac{r_0-r \cos\phi}{r_0^2+r^2-2 r_0 r \cos\phi}d\phi$$

The integrand plots like

Note that

$$ I(r_0,r;0,2\pi)=I(r_0,r;0,\pi)+I(r_0,r;\pi,2\pi) $$ Upon the change of varibale $\phi\to\phi-\pi$ in the second integral above, and then explicitly simplifying, one gets the recursion

$$ \begin{align} I(r_0,r;0,2\pi)&=r_0\int_0^{2\pi}\frac{r_0^2-r^2 \cos\phi}{r_0^4+r^4-2 r_0^2 r^2 \cos\phi}d\phi \\ &=r_0~I(r_0^2,r^2;0,2\pi)\\ \end{align} $$

Therefore $$ \begin{align} I(r_0,r;0,2\pi)&=\lim_{k\to\infty}r_0^{k -1}I(r_0^k,r^k;0,2\pi)\hspace{1cm} k\in1,2,4,8\ldots \end{align} $$

For $r<r_0$, $$ \begin{align} I(r_0,r;0,2\pi)&=\lim_{k\to\infty}\frac{r_0^{k-1} r_0^k}{r_0^{2k}}\int_0^{2\pi}\frac{1-(r/r_0)^k\cos\phi}{1+(r/r_0)^{2k}-2(r/r_0)^k\cos\phi}d\phi \\ &=\frac{2\pi}{r_0} \end{align} $$

For $r_0<r$, $$ \begin{align} I(r_0,r;0,2\pi)&=\lim_{k\to\infty}\frac{r_0^{k-1} r^k}{r^{2k}}\int_0^{2\pi}\frac{(r_0/r)^k-\cos\phi}{1+(r_0/r)^{2k}-2(r_0/r)^k\cos\phi}d\phi \\ &=\lim_{k\to\infty}(r_0/r)^{k-1}\ldots\\ &=0 \end{align} $$

---