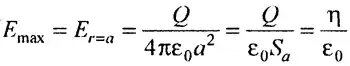3

A sphere of radius $a$ is in the vacuum and it's evenly charged with charge quantity $Q$.

Does an electric field has maximum exactly at the surface ($r = a$) or slightly above the surface ($r = a+0$) of this sphere?

$$E=\begin{cases} 0 &(r < a) \\ \frac{Q}{4\pi\epsilon_0 r^2} &(r \ge a) \end{cases}$$

enter image description here

In my book it says that maximum field is at the surface of the sphere E(r = a) enter image description here enter image description here

In another book(University Physics with Modern Physics by Hugh D. Young, Roger A. Freedman, A. Lewis Ford) it says E for electric field at the surface of a charged conducting sphere enter image description here

asd.123
  • 783
Pavle
  • 33

2 Answers2

3

Using classical approach to solve your problem, there will be an an ambiguity, because of the simple modelling used for the calculation of electrostatic force. In addition, when Gauss' law applied with spherical Gaussian surface for the conducting sphere that you asked result will be ambiguous and inconclusive where the singularity comes into the calculations. On the other hand with more modern approaches, ambiguity can be solved and for this I suggest this pdf where the modelling has altered to overcome ambiguity.

Reference to the external link:

Lima, F. (2018, November). What Exactly is the Electric Field at the Surface of a Charged Conducting Sphere? https://www.ias.ac.in/article/fulltext/reso/023/11/1215-1223

asd.123
  • 783
  • In this example point charge is used – Pavle Sep 20 '20 at 15:38
  • I edited question. In my book it says there is maximum value at the surface of the sphere and in another book it says E for electric field at the surface of a charged conducting sphere @Butane – Pavle Sep 20 '20 at 18:16
  • @Pavle the main reason for the ambiguity is singularity and I suggest to check https://physics.stackexchange.com/q/580865/210249 – asd.123 Sep 20 '20 at 18:54
  • If you accept the problems of classical method it works well for huge area though there will be some peculiarities at certain points – asd.123 Sep 20 '20 at 18:56
  • So with classical approach there will be electric field at the surface of the sphere E(r = a)? @Butane – Pavle Sep 20 '20 at 19:40
  • @Pavle actually classical approach has ambiguity and don't defines anything even if you look at the graph that you provide the electric field function is discontinuous and have two different values at the same distance r. So, this is the approach of the books to ambiguity which is both 0 and maximum accepted. – asd.123 Sep 20 '20 at 19:52
  • Let us continue this discussion in chat. – Pavle Sep 20 '20 at 20:05
  • The answer should have a brief description of the result in the link, not just the link itself. – Dale Sep 21 '20 at 03:36
  • @Dale I didn't give the pdf as the answer it is just a recommendation for further reading because pdf has a different approach than the classical theory where as far as I understood from the question and referring the textbooks I gave the answer for classical approach. – asd.123 Sep 21 '20 at 04:15
2

There is charge exactly at the surface of the shell, so you can't unambiguously define the E-field at that point. One reasonable convention would be to define the electric field at that point by the electric force that is exerted on the charge there. In this case it is a charge per unit area so the electric field would be defined as $E=P/\sigma$.

Since charges do not exert a force on themselves, to find the force on an infinitesimal area, the electric field of the infinitesimal area itself should be excluded. In other words, this result can be obtained by cutting a small hole out of the shell and finding the electric field due to the rest of the shell, excluding that hole.

The E-field exactly at $r=a$ found this way comes out to $E=\frac{Q}{8\pi\epsilon_0 a^2}$, or half the maximum value. The calculation is left as an exercise to the reader.

This is gives the pressure due to the electric force that is felt by the shell as

$$ P=\sigma E=\sigma\frac{Q}{8\pi\epsilon_0 a^2} = \frac{Q}{4\pi a^2}\frac{Q}{8\pi\epsilon_0 a^2}=\frac{Q^2}{32\pi^2\epsilon_0a^4}$$

which agrees with the pressure as calculated with other methods.

The more typical convention is that the electric field is simply undefined at that point. In any case, regardless of convention all the physical measurables (force, pressure, etc) are the same.

Chris
  • 17,189