Why does $g$ vary from a direct square relationship inside the earth to an inverse square relationship above the earth's surface?

Question

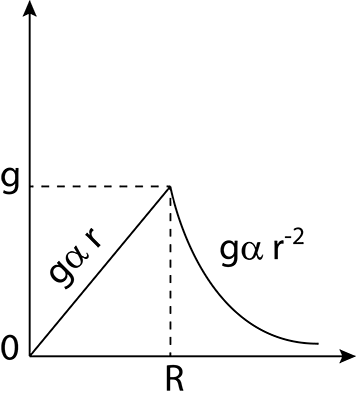
Why does acceleration due to gravity $g$ vary with altitude, height, and depth from a direct square relationship inside the earth (below the earth's surface) to an inverse square relationship above the earth's surface? Further, how did we get the following equations for the below the earth and the above the earth, respectively?

$$ \begin{aligned}g'=g\left[ 1-\dfrac{x}{R}\right] \ldots \left( 1\right) \\ g'=g\left[ 1-\dfrac{2x}{R}\right] \ldots \left( 2\right) \end{aligned} $$

where $g'=g\left[ 1-\dfrac{x}{R}\right]$ is $g$ at depth $x$ and $g'=g\left[ 1-\dfrac{2x}{R}\right]$ is $g$ at altitude $x$.

The relationship between $g$ and depth shown in the graph assumes the Earth has a uniform density. A more accurate relationship is shown in answers to this question. — M. Enns, Oct 15 '22 at 18:42

score 0 · Answer 1 · answered Feb 09 '22 at 13:43

As you approach the surface of the Earth from above all of the mass of the Earth is considered to be at its center ("below" you). But once you go below the surface of the Earth, there is mass both above and below you. The mass above you reduces your acceleration linearly towards the center as you move towards the center.

For a derivation of the equation see here:

https://www.examfear.com/notes/Class-11/Physics/Gravitation/1755/Acceleration-due-to-gravity-below-the-surface-of-earth.htm#:~:text=g%3DF%2Fm%20where%20g,the%20surface%20of%20the%20earth.

Hope this helps.

Why does $g$ vary from a direct square relationship inside the earth to an inverse square relationship above the earth's surface?

1 Answers1