-3

Why the acceleration of free-falling bodies become zero after some time? My only idea would be that the closer to the core of Earth we are, the value of "g" the lower becomes (since the mass below the body is lower and consequently, its gravitational force is also lower) but it works on large scales, like hundreds and thousands of kilometres. (and also, I'm not sure in it)

I don't count with air resistance, since an experiment with checking terminal velocity would work in vacuum too.

EDIT: I thought about enery aspects too, but obviously a body that falls with constantly increasing speed wouldn't be a perpetuum mobile, because once it's gonna reach with the larger body, and then speed becomes zero.

Zoltán Schmidt
  • 210

3 Answers3

4

Terminal velocity exists because a velocity dependent force against gravity results in a net acceleration of 0.

In most cases, air resistance (drag force) is the velocity dependent force.

Out of curiosity, why does terminal velocity work in a vacuum too?

sihrc
  • 213
  • Honestly, I'm not a physicist, but I'm enthuastic at it, and with my logic, if it wouldn't work in vacuum, that'd mean that the speed of asteroids would accelate constantly, and their speed may even come near to the speed of light. But because of the terminal velocity, they can't approach this level of speed. The question is that what is the velocity dependent force that results in a net acceleration of 0, if it's not the air resistance? – Zoltán Schmidt Jul 29 '13 at 18:52
  • +1 for the answer. And it works in vacuum, because if the thing is pulled down, at one point it make Boom! :) – Nikolaj-K Jul 29 '13 at 18:54
  • @ZoltánSchmidt In a vacuum, there is little acceleration to pull the asteroid to begin with. You wouldn't need a resistive force for "terminal velocity" because there isn't acceleration (very little due to gravity over great distances). In this scenario, the acceleration is little, if not none, so the velocity is constant (rather than terminal). If it came close enough to a planet (earth) for gravitational force to "change" the velocity, then it will accelerate more and keep going until BOOM. – sihrc Jul 29 '13 at 18:58
  • But if the gravitational field of the Sun (among enourmous amount of other stars) has so strong gravity field that it can make giant planets orbit around itself, why it can't make either asteroids of these planets accelerate? – Zoltán Schmidt Jul 29 '13 at 19:13
  • @ZoltánSchmidt Large masses do accelerate comets. If there is only one significantly large mass near it, the comet will accelerate towards that mass and probably crash/burn. Comets don't accelerate indefinitely because there are also large masses pulling them in other directions. And as julian frenandez posted, it is also possible that they reach circular motion around large masses. – sihrc Jul 29 '13 at 19:33
  • 1
    @ZoltánSchmidt: You seem to be confused by something else as well. A body can keep accelerating while never reaching the speed of light. See Rindler coordinates. – Raskolnikov Jul 29 '13 at 19:33
1

in the vacuum, and in absence of other frictional forces (electromagnetic, etc), you do not reach terminal velocity for linear motion. An asteroid, is always accelerated, same as a satelite orbiting around the earth. They can reach "constant" speed if they are in a circular motion, but the direction of the speed changes (it is a circular motion), due to the acceleration of gravity. So velocity, is not constant. If you could make a tunnel through the center of the earth and drop a ball, it will keep accelerating until it reaches maximum speed at the center, then it will keep going to the other side, this time decelerating, until it reaches zero speed at the other end of the tunnel and comes back, in an endless oscillatory motion

Akash
  • 103
-2

I assume that you're asking a question about the fundamental physics involved in terminal velocity, then this is a good question.

Terminal velocity exists because at this point a falling object (e.g. rock) displaces a total mass of fluid (e.g. water or air) equal to their own mass, each second. This is similar to the concept of buoyancy for boats and balloons.

At terminal velocity:

Mass of Rock Falling = Total Mass of fluid displaced each second

which is the same as buoyancy for a boat floating in water:

Mass of Boat = Total Mass of fluid displaced each second

This is why the same object must fall a lot further through air than water, at terminal velocity for that fluid. i.e. The rock has to fall through a greater volume of air each second, before displacing the same total mass as compared to water, because air is a lot less dense than water (about 1/1000 times less dense). hence terminal velocity is a lot higher falling through air than water, as the rock falls further before achieving buoyancy. See image:

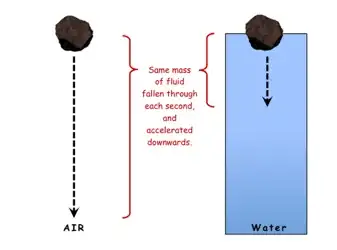
enter image description here

The 'total mass of fluid displaced' includes the fluid directly fallen through and the fluid indirectly displaced by the rock accelerating the fluid fallen through away from it.

Total mass of fluid displaced = Mass of fluid directly displaced + Mass of fluid indirectly displaced.

enter image description here

This approach allows you to calculate the downward force exerted by the rock on the air/water in terms of the mass of fluid ('m') fallen through and its acceleration ('a') i.e. Force = ma).

This is not how they explain it in school textbooks. They will blame things like viscosity of the fluid .... which is only part of the explanation. It misses the 'bigger picture' explanation of the masses involved.

Nick Landell
  • 175