Does the total wave function for distinguishable (i.e. not identical) spin 1/2 fermions need to be anti-symmetric under particle exchange? Or does the Pauli exclusion only hold for indistinguishable fermions?
-
I think it is necessary that you add what is your level of knowledge and what you have tried so far. Any good quantum mechanics books will address this very clearly so maybe we can narrow down where are you exactly blocking with respect to it. – Mauricio Feb 02 '23 at 19:57
-
The Pauli exclusion principle does not make any statement for distinguishable particles. That's why I was stuck to determine the exchange symmetry of the wavefunction. Hope my question is clear now. – Can Sacan Feb 02 '23 at 20:00
-
Have you checked other content on the topic of (in)distinguishable particles in quantum mechanics? – Mauricio Feb 02 '23 at 20:09
-
I am sorry but you are not helping me understand the relevant information, but rather trying to test my knowledge on the topic. Yes if you are curious I have also checked the exchange symmetry of N particles and the Wronskian determinant to calculate anti-symmetric wave-functions of an N-body system. Don't see how asking these questions are relevant... – Can Sacan Feb 02 '23 at 20:20
-
Sometimes showing more details can allow us to narrow down where is the issue. For example pinpointing an equation or page in a book can make it more clear what are you interpreting correctly and what not. Demonstrating that you know about the subject also allows for a more adequate response to your level and avoiding answers that are either too technical or too simplistic. – Mauricio Feb 02 '23 at 20:25
2 Answers
Quoted from Pauli exclusion principle (emphasis by me):
A more rigorous statement is that, concerning the exchange of two identical particles, the total (many-particle) wave function is antisymmetric for fermions, and symmetric for bosons. This means that if the space and spin coordinates of two identical particles are interchanged, then the total wave function changes its sign for fermions and does not change for bosons.
- 39,317
-
This unfortunately does not answer my question, I am asking for NOT identical particles (distinguishable) – Can Sacan Feb 02 '23 at 19:58
-
2
-
Yes I know thank you, but I am asking for the case when the particles are distinguishable, say they have opposite charge or different mass or whatever. Your answer concerns indistinguishable/identical particles. I am asking for distinguishable/non-identical particles – Can Sacan Feb 02 '23 at 20:02
-
1Particles are either distinguishable or indistinguishable. The answer to your question is not literally typed out in this answer, but it is clear from this answer. Not sure what the gripe is. If you want someone to explicitly answer your exact question, you can see my answer. – hft Feb 02 '23 at 20:07
No. Particles may be indentical but may or may not be indistinguishable. Indistinguishable particles will be described by a quantum state fully symmetric or fully antisymmetric under permutation.
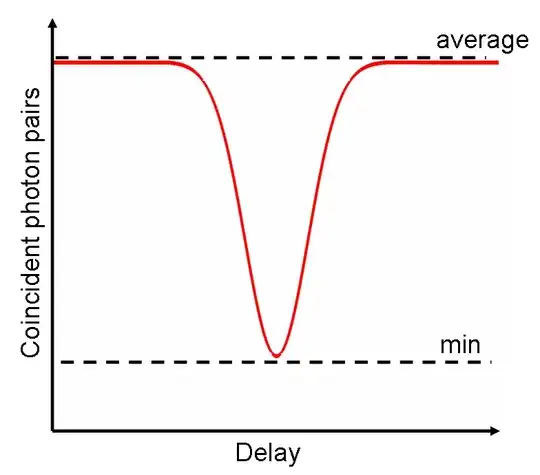
It is perfectly possible to have partially distinguishable particles: two photons with non-orthogonal polarization made to interact at a beam splitter are an example of system of partially distinguishable particles. If the photons are described by wave packets, then the overlap of the wave packets serves as a measure of distinguishability. The most spectacular example of this is the Hong-Ou-Mandel effect, where certain coincidence rates basically go to 0 only when the photons are fully indistinguishable:
In the figure, the overlap between two Gaussian wave packets is tuned using an ajustable delay. When the two packets overlaps and the photons are fully indistinguishable, there is no probability of the two photons exiting to different ports of the interferometer. As one increases the distinguishability, this probability increases.
If you’re looking for an example with two fermions, imagine two wave packets describing identical spin-1/2 fermions but such that the wave packets are only partially overlapping. In this case the state is described by a linear combination of a fully symmetric state, and a fully antisymmetric state (here we’re talking about symmetric/antisymmetric w/r to the action of the permutation group $S_2$), and the coefficients are such that, as the wave packets fully overlap, only the antisymmetric combination remains. Indeed the HOM experiment has been done with electrons, as reported in
Liu, R. C., et al. "Quantum interference in electron collision." Nature 391.6664 (1998): 263-265
and in
Oliver, William D., et al. "Hanbury Brown and Twiss-type experiment with electrons." Science 284.5412 (1999): 299-301.
Note the similarity between the results of Oliver:

and the results of Hong et al.
- 45,515