3

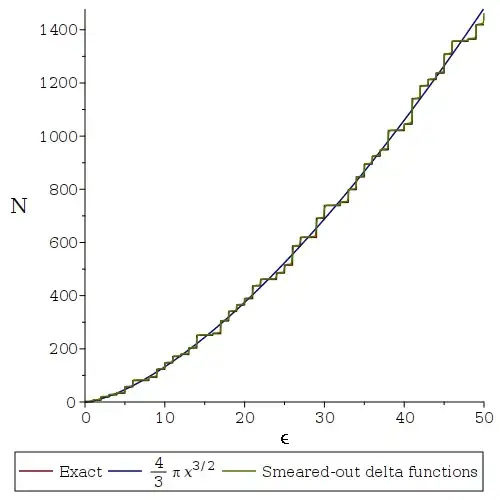
In most basic statistical physics/condensed matter discussion the density of states is used to convert a discrete sum to a continuous integral

$$\sum_{\alpha} \mapsto \int d\epsilon \ g(\epsilon).$$

For example, a common derivation of the density of states can be done by considering the volume of a sphere in $k$-space (corresponding to the total number of states with wavevectors $<k$) and then taking the derivative e.g. Wikipedia - k-space topologies.

However under what conditions is this accurate?

Indeed, the continuous density of states method breaks down for Bose-Einstein condensates because the density of states

$$ g(\epsilon) = \frac{\sigma}{4 \pi^2} \left( \frac{2m}{\hbar^2} \right)^{3/2} \sqrt{\epsilon} $$

gives no weight to the states at $\epsilon = 0 $ since $g(\epsilon) \propto \sqrt{\epsilon}$.

For example, jacob1729's answer here describes that

One option for this is of course $g(\epsilon)=\sum_{\alpha}\delta(\epsilon-\epsilon_\alpha)$ but in practice this might be smeared out a little whilst not hurting the approximation (eg convolve with a Gaussian of width $\Delta\ll kT$).

This is an approximation. We expect this approximation to become exact as the level spacing goes to zero under the assumption that the states do not become macroscopically occupied.

My questions

  • How can we justify/quantify the statement "under the assumption that the states do not become macroscopically occupied" and what are the mathematical conditions for the convergence of the integral?
  • In the derivation using $k$-space topologies, where is the assumption that the density of states cannot be small made? In the case of the Bose-Einstein condensates, if this density of states is wrong at $\epsilon = 0$ why does it work at all for larger energies?

The question How to prove that sum converges to integral using density of states? appears relevant but I still don't understand why the density of states fails for low energy states (for example, as in Bose-Einstein condensates).

user246795
  • 592
  • This is more math than physics. An integral is not just the sum of cases. An integral must start out as a sum of a function of a variable times the step between the summed cases. The differential must be defined. Take the limit as the steps approach zero and the number of steps approaches infinity. You cannot integrate one step. Define your differential, and define the boundaries. Once done, an integral converges if the limit exists. The limit covers the range between the endpoints. If there is a discontinuity at either endpoint, it does not affect the integral. – Ken Mellendorf Apr 13 '23 at 20:04
  • In the case of Bose-Einstein condensation, it seems to me that the problem is not that the density of states is small at $\epsilon = 0$, but rather that the ground-state becomes macroscopically occupied. These two things just happen to occur at the same time. – Jakob KS Apr 14 '23 at 11:18
  • @JakobKS But I do not understand why the groundstate cannot become macroscopically occupied in our density of states integral formulation. Where did we make the assumption that no state was macroscopically occupied? What is the definition of macroscopically occupied? – user246795 Apr 14 '23 at 14:12
  • I was typing a reply, but ended up making it an answer instead. I hope this helps answer your question! – Jakob KS Apr 14 '23 at 16:21

2 Answers2

2

The energy levels of bound states in a quantum system are always discrete, and so expressions like $g(\epsilon) \propto \sqrt{\epsilon}$ are always an approximation. How well such an approximation will work depends on what you're trying to calculate, and what approximation you are using. It is hard to say anything more general than that, other than a general word of caution that extra care should be taken if the function you are trying to evaluate has singularities (like the Bose-Einstein distribution in the limit $\epsilon \rightarrow \mu$).

We are so accustomed to seeing these continuous approximations for the density of states that one easily forgets that they are (1) not exact and (2) not unique.

An example might be helpful. Let us take the system you described of a 3D gas of free non-interacting particles confined to a box of dimensions $L\times L \times L$. We know that we will have eigenenergies $$\epsilon_k = \frac{\hbar^2}{2m} (k_x^2 + k_y^2 + k_z^2),$$ and that the allowed $k$ values will be discretized by the boundary conditions $k_\alpha L = 2\pi n$, where $n\in\mathbb{Z}$ and $\alpha \in \{x,y,z\}$.

As an example, assume that we want to calculate the counting function $N(\epsilon)$ which counts the total number of states below an energy $\epsilon$. We can calculate this as $$N(\epsilon) = \sum_k \theta(\epsilon - \epsilon_k) = \int_0^\epsilon d\epsilon' g(\epsilon') \theta(\epsilon - \epsilon'),$$ where $g(\epsilon) = \sum_k \delta(\epsilon - \epsilon')$ is the (exact) density of states.

Let us do this numerically to test various continuous approximations to the DOS. I'll set $2m = 1$, $\hbar = 1$ and $L = \frac{1}{2\pi}$ to make all the annoying numerical constants drop out. Then we have $$\epsilon_k = k_x^2 + k_y^2 + k_z^2 = n_x^2 + n_y^2 + n_z^2.$$ The normal approach to approximating the density of states as a continuous function would result in $g(\epsilon) \approx 2\pi \sqrt{\epsilon}$ which would then result in $N(\epsilon) \approx \frac{4\pi}{3} \epsilon^{3/2}$. We could also make another approximation by replacing the delta-functions in the exact DOS by narrow Lorentzians $\delta(\epsilon) \approx \frac{\eta}{\pi(\epsilon^2 + \eta^2)}$ for some small $\eta$.

In the three figures below I've calculated $N(\epsilon)$ using the exact DOS and the two approximation schemes outlined above (for the smeared deltas, I set $\eta = 0.02$). The only difference between the figures is the range shown on the x- and y-axes.

From the figures it is quite clear that the ordinary continuous approximation becomes very good at large energies, when there are many contributing states, but is not so great for low energies when only a smaller number of states contributes to the sum. From this we can infer that for this system, we can safely use $g(\epsilon) \approx 2\pi \sqrt{\epsilon}$ if the main contribution to the sum comes from the multitude of states at high energies. However if a single state by itself contributes significantly to the sum, it is necessary to have a very good approximation to $g(\epsilon)$ for that particular state. If you have a macroscopically occupied state in your system, it is likely to contribute significantly by itself to any function that you are trying to calculate, and in that case the approximation you are using must take that into account.

enter image description here

enter image description here

enter image description here

Jakob KS
  • 1,723
  • 5
  • 16
  • This makes things so much clearer! So can this entirely explain the "mistake" in the case of Bose-Einstein condensation? Our usual approximation to the DoS $g(\epsilon) \propto \sqrt{\epsilon}$ clearly does not count states with $\epsilon = 0$. But the exact delta function DoS does include the ground states due to the $\delta(\epsilon -0)$ term (when all $n_{x,y,z}=0$). And using your "counting (step) functions" $\theta(\epsilon-\epsilon_k)$, clearly the ground state is included since $N(0) = 1$. – user246795 Apr 14 '23 at 17:39
  • But in this case of a Bose gas the "counting function" is the Bose-Einstein distribution $n(\epsilon_k) =\frac{1}{e^{\beta(\epsilon_k -\mu)}-1}$ (instead of the step functions). When working with the exact DoS, the first delta function $\delta(\epsilon)$ would pick-out the term $N_{0} =\frac{1}{e^{-\beta\mu}-1}$ where as our approximate $g(\epsilon) \propto \sqrt{\epsilon}$ doesn't. And this is the explicitly reason for why we split the number of particles into $N = N_0 + N_{\epsilon >0}$ when solving for the number of particles in the ground state of a condensate? – user246795 Apr 14 '23 at 17:39
  • Yes, that is exactly it. And as all the excited states have a very low occupancy at low temperature, the error made by using the approximate $g(\epsilon)$ is vanishingly small for these states. – Jakob KS Apr 14 '23 at 18:44
  • But also the (percentage/relative) error for our approximate $g(\epsilon)$ becomes increasingly small for the larger energy excited states, regardless of occupancy? – user246795 Apr 14 '23 at 18:52
  • The relative error becomes smaller, but I don't think the absolute error does. Looking at the numerical analysis, the relative error in measured as $\frac{N_\mathrm{exact} - N_\mathrm{approx}}{N_\mathrm{exact}}$ becomes smaller for larger energies, which can also be seen in the three figures above. However the absolute error $|N_\mathrm{exact} - N_\mathrm{approx}|$ seems on average to grow slightly with higher energies. Is that what you meant? – Jakob KS Apr 14 '23 at 19:00
  • I did mean that the relative error decreases. Intuitively it seems reasonable that the approximate density of states $g(\epsilon)$ does not work for low energies because the relative error from the exact count $N$ is high. But for larger energies the difference between, for example, $N(\epsilon){\text{exact}} = 1114$ and $N(\epsilon){\text{approx.}} = 1114.529 \ldots$ is less of an issue? Or is the absolute error important....? – user246795 Apr 14 '23 at 19:13
1

How can we justify/quantify the statement "under the assumption that the states do not become macroscopically occupied" and what are the mathematical conditions for the convergence of the integral?

I think @JacobKS h=gave a good answer to this, but I would like to restate it somewhat differently. The derivation assumes an idealized situation, ignoring many of the real-sample effects, among which are:

  • the interactions leading to establishment of thermodynamic equilibrium, which means that the states are broadened
  • the finite size of the sample
  • presence of interactions, which may contribute to both of the above: giving finite lifetime to the particles (i.e., level broadening) and producing a gap (i.e., finite separation between states.)

By converting sum to the integral we assume that the gaps between the states, which are due to the finite sample size (or possibly interactions) are smaller than the broadening of the states. This might not be always the case, and we do observe the contrary in case of Bose-Einstein condensation or superconductivity.

In the derivation using k-space topologies, where is the assumption that the density of states cannot be small made? In the case of the Bose-Einstein condensates, if this density of states is wrong at ϵ=0 why does it work at all for larger energies?

In this argument we divide the phase space into cells (e.g., using periodic boundary conditions) and then count the number of cells in a unit sphere. Without this discretization the number of states would be infinite. However, the discretization means that we count the number of states inside approximately - easy to see, if we consider, e.g., cubic sells with sides $\frac{2\pi}{L_x}, \frac{2\pi}{L_y}, \frac{2\pi}{L_z}$. This approximation becomes exact only when we take limit of $L_x,L_y,L_z\rightarrow \infty$, but this is the same as converting the sum into integral.

Roger V.
  • 58,522