3

When researching robots, micro mouses etc I've often come across people taking about generating "speed profiles" and how to calculate them. Also profiles for acceleration , deceleration , turning etc. Also trapezoidal profile?

But I can't seem to find exactly what is meant by this. The how or why also.

So what is a "profile" in this sense and why you would need one?

binarysmacker
  • 145
  • 1
  • 5

2 Answers2

6

Think of a motion profile as a graph of speed vs. time.

If you drive your car down the road:

  • Your initial speed is zero.
  • You start pressing the accelerator pedal.
  • The car starts moving slowly.
  • You keep pressing down on the accelerator.
  • The car accelerates faster.
  • As you approach your targer speed you let go of the accelerator.
  • The car settles on your target speed.
  • You approach a stop sign and start pressing on the brake pedal.
  • Your speed goes down and as you approach the stop sign you start letting go of the brake pedal.
  • You come to a smooth stop.

I just described roughly what people would refer to as an S-curve motion profile or a limited jerk profile. To experience jerk in your car try this next time you stop, press the brake pedal but do not let it go at all until the car comes to an absolute stop. This also illustrates the importance of controlling the motion profile for smooth motion. When graphed this looks something like this:

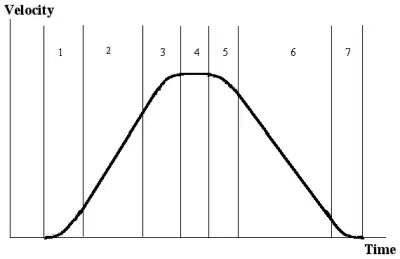
Wikipedia third order motion profile

You can see the S in there. A trapezoidal profile has straight lines and three sections and as per our car experiment above will force you to reduce your acceleration to avoid "jerking" at the "corners" (discontinuities).

You should also think about this in terms of the equivalent position vs. time graph. A motion profile executed in a robot, e.g. is typically moving from one position to the other.

Motion profiles are critical for achieving smooth and reliable high performance motion. With more than one motion axis they are also important for synchronizing the motion. Without them your motion might look like your car firing off a rocket to get started and locking the wheels to stop at the end of the street, not very pretty.

Additional reading:

https://www.pmdcorp.com/resources/get/mathematics-of-motion-control-profiles-article

Jaroslav Klapálek
  • 3
  • 2
Guy Sirton
  • 1,090
  • 6
  • 9
  • Thanks guy! That's some good information. Another question however is about physically implementing it and what it means. So after making a profile you have the ideal movement for maximum speed and smoothness?...but then what do you do with this?. Would you have a timer on your microcontroller monitoring the time and adjusting the speed to match your profile? People talk about this profiles as a table also. Is this just tovavoid computing the profile in real time? – binarysmacker Mar 16 '14 at 12:51
  • @binarysmacker: You typically already have a closed-loop (PI) controller for position and velocity at this point. A timer can then be used to set the profile as the input for the controller. Also yes, a table can be used to avoid making these calculations on the fly. – Guy Sirton Mar 16 '14 at 18:18
  • But also, I cant see the difference in calculating and implementing a profile and with how I am doing it. How im moving my robot, say I have to move it 500 encoder ticks. I just say from 0 to 100 ticks, speed = speed + 1 then its constant, then at 400 ticks speed = speed - 1. Unless by doing this im creating an implicit profile? But then if I am, what benefit would there be if I was to calculate a curve? – binarysmacker Mar 16 '14 at 22:01
  • 2
    @binarysmacker Yes. You are creating a trapezoidal profile. You will get a smoother motion if you calculate an S-curve: speed = speed + accel accel = accel + x. Also how do you change your acceleration and speed in your current code? What happens when you make a move shorter than 200 ticks? – Guy Sirton Mar 16 '14 at 23:56
  • Well, I just gave that as a quick example but if it's shorter than 200 ticks it turns the profile into a triangle shape as it never gets to a constant speed. So it goes straight into deccelaration from acceleration. So, what are you trying to achieve when you calculate a profile rather than just doing what I do or implementing the code you suggested. Why would people be using tables when the code you showed is light weight anyway. – binarysmacker Mar 17 '14 at 13:30
0

You can use this code in MATLAB:

x = 0:0.1:20;
y = dsigmf(x,[1 4 1 16]);
plot(x,y)

Or

clc
clear all;

speed=600;
step=300;


for i=0:1:step
  y1(i+1)=1/(1+exp(-(0.05)(i-100)));
  y2(i+1)=1+(-1/(1+exp(-(0.05)(i-200))));
end


y=[y1,y2];
plot(y)
xlabel('time(Step)')
ylabel('Speed')
xlim([-0.05 600])
Mohammad Sabouri
  • 1
  • Welcome to Robotics Mohammad Sabouri. Thanks for your answer but we are looking for comprehensive answers that provide some explanation and context. A dump of uncommented code cannot do this, so please edit your answer to explain why it is right, ideally with citations. Answers that don't include explanations may be removed. See [answer] for more info. – Ben Oct 13 '21 at 14:16