4

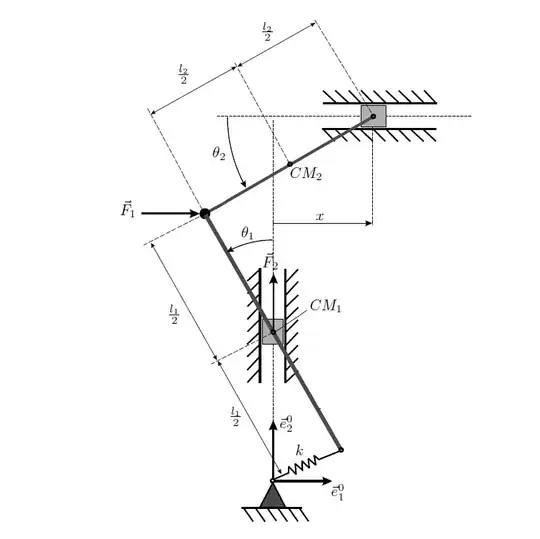
I'm working on an assignment and was wondering aobut the degrees of freedom this system has. The generalized coordinates are: $\underline{q}:$ \begin{bmatrix} x \\ \theta_{1} \\ \theta_{2} \\ \end{bmatrix} A revolute joint connects both rods. Furthermore, there is a horizontal actuation force $F_{1}$ in the revolute joint and a vertical actuation force $F_{2}$ in $CM_{1}$

I know that there are 2 bodies so 6 DOF in total. The revolute joint constraints 2 DOF, and both sliders also constrain 1 DOF each. The actuation focres also remove 1 DOF each. which means that the total number of DOF is $0$. Is this correct?

I'm not sure what the spring at the bottom does.

Thanks in advance for any helpenter image description here

abraham lincoln
  • 41
  • 1

1 Answers1

3

The system has 2 DOF! Your assumption The actuation focres also remove 1 DOF each. is wrong.

Generally you can always use a simple proof about the DOF. In your system you have 3 generalized coordinates. If you fix one of them (e.g. the $x-$coordinate) you can still move the joint via $F_1$. The angles $\theta_1, \theta_2$ would change then. If you fix another coordinate, lets say $x$ and $\theta_1$ you will not be able to move anything in the system anymore. Therefore the system has 2 degrees of freedom.

madn
  • 189
  • 7