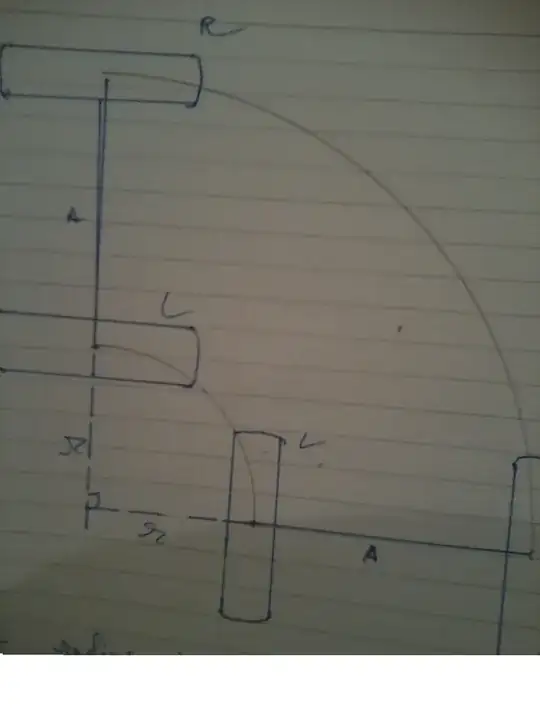
I want to give my robot a differential mechanism for the system of turning and steering. Considering the case of turning a right-angled corner, the robot will achieve this by following a gradual circular arc through the intersection while maintaining a steady speed. To accomplish this end, we increase the speed of the outer wheel while slowing that of the inner. But supposing i want the turn to be within a definite radius, how do i calculate what ratio the 2 speeds have to be in? Can someone give me an insight into this?
What Ive done is this, although I have my doubts.
If the speed of the right wheel is $V_r$ and the speed of the left wheel is $V_l$, then the ratio of their speeds while turning will be equal to the ratio of the circumferences of their corresponding quadrants.
Therefore $$V_r :V_l =\frac{r+A}{r}$$
Is this right? I have a sinister feeling Im missing something out..