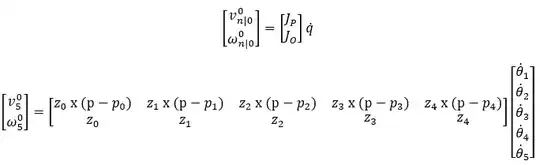5

I am modelling an articulated robot arm with 5 degrees-of-freedom from igus (igus Robolink).

I deduced its direct kinematics equations using Denavit-Hartenberg parameters and homogeneous transformation matrices. I also calculated its Jacobian and inverse kinematics problem of position.

Now I am bit stuck with the problem of inverse velocity. Since the Jacobian is a [6x5] matrix and can't be inverted directly, could you tell me any way to invert it, i.e. Pseudo-Inverse matrix? Or is there a better way to solve inverse velocity problems for 5 DOF robots rather than with the Jacobian?

enter image description here

Greenonline
  • 1,508
  • 4
  • 18
  • 32
João Sobral
  • 51
  • 4
  • It might help if you type out all of your equations. – Paul Oct 02 '18 at 20:33
  • Already added equations. It is general solution for direct velocity. My point regarding inverse velocity is a way to invert jacobian. – João Sobral Oct 03 '18 at 14:11
  • It would be much better if you attach a picture of the robot. Also it might be possible to get velocity inverse kinematics from that of position. – AlFagera Oct 14 '18 at 06:32

2 Answers2

2

I remember two possibilities:

  • As you already said: inversion of the Jacobi matrix. You can maybe look for Moore-Penrose on this topic.

  • derivation in joint space. If you already solved the inverse problem, and $q$ is known, you can just derivate the position signal:
    $\dot q = \frac{d q}{dt}$

I would prefer the second method. If you want to use the pseudo-inverse you have to check the condition of the matrix. Your pseudo-inverse may become singular. Since you usually have to solve the coordinate transformation of the position signal $q$ anyway, this is way more efficient. You need no matrix operations. For a discrete signal (with sample Time $T$) you can approximate the velocity signal with:

$ \dot q(i) = \frac{q(i+1) -q(i)}{T}$

stoeppsel
  • 56
  • 3
1

You might solve the inverse kinematic problem using the derivation as above. However, I would recommend to solve with Jacobians (Pseudo-inverse matrix). If you are modelling a robot arm, you might have to deal with the classical problems such as collision avoidance or joint-limit problem. One big advantage of the Pseudo-inverse matrix is that you can easily modify it to solve these classical problems.

Joe
  • 324
  • 1
  • 10