Calculate position of differential drive robot

Question

How do you calculate or update the position of a differential drive robot with incremental sensors?

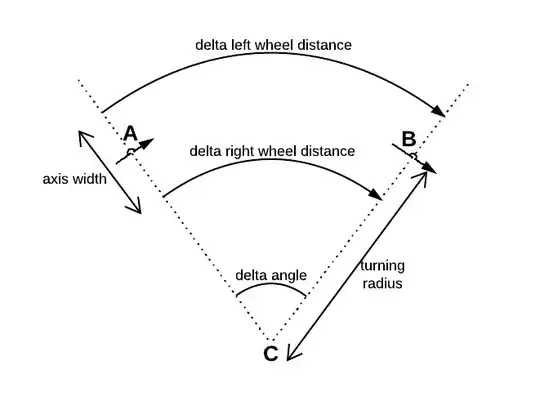
There is one incremental sensor attatched to each of the two differential wheels. Both sensors determine the distance $\Delta left$ resp. $\Delta right$ their wheel has rolled during a known time $\Delta t$.

First, let's assume the center between both wheels marks the position of the robot. In this case, one could calculate the position as:

$$ x = \frac{x_{left}+x_{right}}{2} \\ y = \frac{y_{left}+y_{right}}{2} $$

"Deriving" those equations under the assumption that both wheels rolled in a straight line (which should be approximately correct for small distances) I get:

$$ \frac{\Delta x}{\Delta t} = \frac{1}{2}\left( \frac{\Delta left}{\Delta t} + \frac{\Delta right}{\Delta t}\right)cos(\theta) \\ \frac{\Delta y}{\Delta t} = \frac{1}{2}\left( \frac{\Delta left}{\Delta t} + \frac{\Delta right}{\Delta t}\right)sin(\theta) $$

Where $\theta$ is the angle of orientation of the robot. For the change of this angle I found the equation

$$ \frac{\Delta \theta}{\Delta t} = \frac{1}{w} \left( \frac{\Delta left}{\Delta t} - \frac{\Delta right}{\Delta t}\right) $$

Where $w$ is the distance between both wheels.

Because $\Delta x$ and $\Delta y$ depend on $\theta$, I wonder whether I should first calculate the new $\theta$ by adding $\Delta \theta$ or if I should rather use the "old" $\theta$ ? Is there any reason to use one over the other?

Then, let's now assume the center between both wheels does not mark the position of the robot. Instead I want to use a point which marks the geometric center of the robot's bounding box. Then $x$ and $y$ change to:

$$ x = \frac{x_{left}+x_{right}}{2} + l\, cos(\theta)\\ y = \frac{y_{left}+y_{right}}{2} + l\, sin(\theta) $$

"Deriving" the first gives:

$$ \frac{\Delta x}{\Delta t} = \frac{1}{2}\left( \frac{\Delta left}{\Delta t} + \frac{\Delta right}{\Delta t}\right)cos(\theta) - l\,sin(\theta)\,\frac{\Delta \theta}{\Delta t} $$

Now there is a dependance on $\Delta \theta$. Is this a reason to use the "new" $\theta$ ?

Is there any better method to do simulatenous update of position and orientation? May be using complex numbers (same approach as with quaternions in 3D?) or homogeneous coordinates?

Answer 1

To answer your first question: if you really want to find the true kinematic equations for differential drive, I wouldn't start approximating by assuming that each wheel has moved in a straight line. Instead, find the turning radius, calculate the center point of the arc, and then calculate the robot's next point. The turning radius would be infinite if the robot is moving straight, but in the straight case the math is simple.

So, just imagine that over each time step, or each time you calculate the change in the incremental sensors, the robot travels from point A to point B on an arc like this: Here's some sample code with the math simplified:

// leftDelta and rightDelta = distance that the left and right wheel have moved along
//  the ground

if (fabs(leftDelta - rightDelta) < 1.0e-6) { // basically going straight
    new_x = x + leftDelta * cos(heading);
    new_y = y + rightDelta * sin(heading);
    new_heading = heading;
} else {
    float R = unitsAxisWidth * (leftDelta + rightDelta) / (2 * (rightDelta - leftDelta)),
          wd = (rightDelta - leftDelta) / unitsAxisWidth;

    new_x = x + R * sin(wd + heading) - R * sin(heading);
    new_y = y - R * cos(wd + heading) + R * cos(heading);
    new_heading = boundAngle(heading + wd);
}

I used similar math in a simulator to demonstrate different ways of steering: http://www.cs.utexas.edu/~rjnevels/RobotSimulator4/demos/SteeringDemo/

Answer 2

For a repeated calculation, it doesn't matter whether you find $\Delta\theta$ before or after you apply $\theta$ to the $\Delta{x}, \Delta{y}$ calculation. You will always be alternating between a position and an orientation calculation.

In a practical sense, it might be better to calculate $\Delta\theta$ after you calculate $\Delta{x}, \Delta{y}$, since your first iteration through the loop requires an initial value of $\theta$.

Remember that this is an error-prone measurement method anyway -- it's a pair of 1D measurements feeding a 2D approximation of a 3D world. Even if you are able to get a $\Delta{t}$ very close to $0$, it still won't account for wheel slippage and uneven terrain.