I am trying to find how much an engine would turn until it stops accelerating with an acceleration of $a = A \sin^2(x)$.
Acceleration
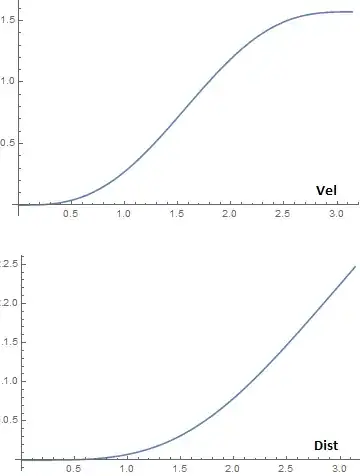
Integrating the acceleration I get velocity $v = A(x/2 - \sin(2x)/4) $
Integrating the velocity, I get the distance $d = A(x^2/4 - \cos^2(x)/4) $
Velocity and distance
Now, I need to do this calculation on a microcontroller, without using floating point and with a sine look-up table which is basically a $2048\sin(x\pi/512)$ function.
How can I find the distance correctly using the sine look up table? Or what other way could I use?

256in the case of your table).... – horchler Aug 04 '15 at 21:14