Finite difference for mixed derivatives on nonuniform grid

Question

I need to have a finite difference stencil for the mixed derivative $$f_{xy}$$

on nonuniform grids such as this one:

Since I could not find a stencil in the literature, I tried to derive it by my self. As usual I started with a Taylor series expansion:

$(I)\qquad f(x+b,y+d)\approx f + b f_x+d f_y +\frac{b^2}{2}f_{xx} +bdf_{xy} +\frac{d^2}{2}f_{yy}$ $(II)\qquad f(x+b,y-c)\approx f + b f_x-c f_y +\frac{b^2}{2}f_{xx} -bcf_{xy} +\frac{c^2}{2}f_{yy}$ $(III)\qquad f(x-a,y-c)\approx f - a f_x-c f_y +\frac{a^2}{2}f_{xx} +acf_{xy} +\frac{c^2}{2}f_{yy}$ $(IV)\qquad f(x-a,y+d)\approx f - a f_x+d f_y +\frac{a^2}{2}f_{xx} -adf_{xy} +\frac{d^2}{2}f_{yy}$

I would like to find a combination of the equations above ($I - IV$) where all derivative terms on the right hand side ($f_x, f_y, f_{xx}, f_ {yy}$) except the mixed derivative vanish. This leads to the following linear system of equations:

$\begin{bmatrix} bf_x && bf_x && -af_x && -af_x \\ df_y && -cf_y && -cf_y && df_y \\ \frac{b^2}{2}f_{xx} && \frac{a^2}{2}f_{xx} && \frac{a^2}{2}f_{xx} && \frac{a^2}{2}f_{xx}\\ \frac{d^2}{2}f_{yy} && \frac{c^2}{2}f_{yy} && \frac{c^2}{2}f_{yy} && \frac{d^2}{2}f_{yy} \end{bmatrix}$ $\begin{bmatrix} P \\ Q \\ R \\ S \end{bmatrix}$ = $\begin{bmatrix} 0 \\ 0 \\ 0 \\ 0 \end{bmatrix}$

A solution to this problem is $P=1, Q=-1, R=1, S=-1$.

Multiplying the equations $I,II,III,IV$ with the respective factors $P,Q,R,S$ and adding them together:

$f(x+b,y+d) - f(x+b,y-c) + f(x-a,y-c) - f(x-a,y+d) = (bd + bc + ac +ad)f_{xy}$

And thus:

$f_{xy} = \frac{f(x+b,y+d) - f(x+b,y-c) + f(x-a,y-c) - f(x-a,y+d)}{bd + bc + ac +ad}$

Can anybody assure me that this is a correct stencil for the mixed derivative for nonuniform grids? What worries me a little bit is that the individual terms ($f(x+b,y+d)$ etc.) do have a uniform weight. So the value at $x+b,y+d$ has equal weight as the point $x-a,y-c$ even though the latter is much closer to the center point $(x,y)$.

Answer 1

My old answer has been edited in a way that I cannot agree with, but AG took such care to type everything out that Ill start again. This is a very old difficulty and the best textbook is Strang and Fix, An analysis of the Finite Element Method, Prentice Hall 1973 (I said it was old) The question was about finite differences, but the issue is the same.

You cannot match a Taylor series consistently to any order because with nine data points you have three points too many for a second-order expansion and one too few for a third-order one. The Finite Element approach, which is more rigorous and systematic than finite differences, assumes that the unknown function is drawn from some specific class of functions (called basis functions, usually polynomials or Fourier modes) The assumption that I make (incomplete quartic, or biquadratic) is standard and makes the most symmetric choice possible. This helps with things like rotational invariance. It may help to notice that along any straight line the function is quadratic in that coordinate, which explains the name. You cannot include a term like $x^3$ because you have no information relating to it. So assume that the unknown function is $$f(x,y)=a_{0,0}+a_{1,0}x+a_{0,1}uy+a_{2,0}x^2+a_{1,1}xy+a_{0,2}y^2+a_{2,1}x^2y+a_{1,2}xy^2+a_{22}x^2y^2$$ where I choose a notation that avoids suggesting a Taylor expansion, and merely defines a chosen interpolating function. Fitting this function to the data gives 9 equations in nine unknowns. Thanks to MAPLE these can be solved for all of the coefficients, and one of these is $$a_{1,1}={\frac {a-b}{ \left( c+d \right) ab} \left( {\frac {d{\it u_7}}{c}}-{ \frac {c{\it u_3}}{d}} \right) }+{\frac {c-d}{ \left( a+b \right) cd} \left( {\frac {b{\it u_5}}{a}}-{\frac {a{\it u_1}}{b}} \right) }-{ \frac {1}{ \left( c+d \right) \left( a+b \right) } \left( {\frac {ad{ \it u_8}}{bc}}+{\frac {bc{\it u_4}}{ad}}-{\frac {bd{\it u_6}}{ac}}-{ \frac {ac{\it u_2}}{bd}} \right) }+{\frac { \left( c-d \right) \left( a-b \right) {\it u_0}}{dcab}} $$ My notation is that $u_0$ is the value at the origin, $u_1$ is the value at $x=b,y=0$, and all other data is numbered anticlockwise around the square.

Because this formula would be exact if the data were quadratic it is second-order accurate. It cannot be third-order because we cannot satisfy all the possible cubic terms. If this formula is used to predict the mixed derivative at any location except the origin of coordinates, it is only first order accurate. At the center, the correct second-order expression is $$u_{xy}(NOT\:\: a_{1,1}!)={\frac {{\it u_2}}{ \left( c+d \right) \left( a+b \right) }}-{\frac {{ \it u_4}}{ \left( c+d \right) \left( a+b \right) }}+{\frac {{\it u_6}}{ \left( c+d \right) \left( a+b \right) }}-{\frac {{\it u_8}}{ \left( c +d \right) \left( a+b \right) }} $$ I do hope that I have managed to make things clearer this time.

Answer 2

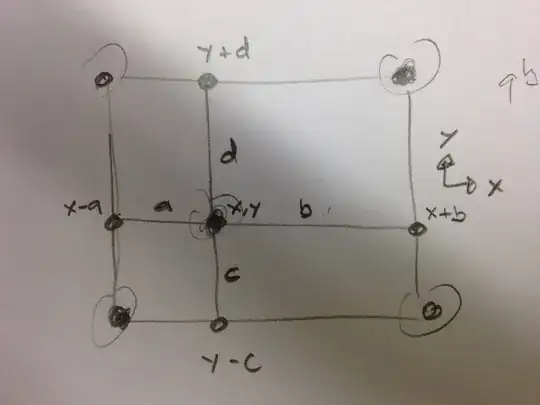
Here we shall follow two procedure to calculate $f_{xy}$ one using Taylors series and another using polynomial fitting. Though both the procedure end up in the same formulation there is some advantages and disadvantage for each one.

Using Taylors series: The advantage of this procedure is: having control over truncation error is easy because we can easily decide what order we want by choosing the order equations that we desired. Programming this is slightly tedious than polynomial series.

Let's expand all the points using Taylors series will end up in

$(I)\qquad f(x+b,y+d)\approx f + b f_x+d f_y +\frac{b^2}{2}f_{xx} +bdf_{xy} +\frac{d^2}{2}f_{yy} + \frac{b^3}{6}f_{xxx} + \frac{d^3}{6}f_{yyy} + \frac{1}{2} b^2df_{xxy}+ \frac{1}{2} d^2bf_{xyy} +\frac{1}{4} d^2b^2f_{xxyy}$ $(II)\qquad f(x+b,y-c)\approx f + b f_x-c f_y +\frac{b^2}{2}f_{xx} -bcf_{xy} +\frac{c^2}{2}f_{yy}+ \frac{b^3}{6}f_{xxx} - \frac{c^3}{6}f_{yyy} - \frac{1}{2} b^2cf_{xxy}+ \frac{1}{2} c^2bf_{xyy}+\frac{1}{4} c^2b^2f_{xxyy}$ $(III)\qquad f(x-a,y-c)\approx f - a f_x-c f_y +\frac{a^2}{2}f_{xx} +acf_{xy} +\frac{c^2}{2}f_{yy}- \frac{a^3}{6}f_{xxx} - \frac{c^3}{6}f_{yyy} - \frac{1}{2} a^2cf_{xxy}- \frac{1}{2} a^2cf_{xyy}+\frac{1}{4} a^2c^2f_{xxyy}$ $(IV)\qquad f(x-a,y+d)\approx f - a f_x+d f_y +\frac{a^2}{2}f_{xx} -adf_{xy} +\frac{d^2}{2}f_{yy}- \frac{a^3}{6}f_{xxx} + \frac{d^3}{6}f_{yyy} + \frac{1}{2} a^2df_{xxy}- \frac{1}{2} a^2df_{xyy}+\frac{1}{4} d^2a^2f_{xxyy}$

$(V)\qquad f(x,y+d)\approx f +d f_y +\frac{d^2}{2}f_{yy} + \frac{d^3}{6}f_{yyy} $

$(VI)\qquad f(x,y-c)\approx f -c f_y +\frac{c^2}{2}f_{yy} - \frac{c^3}{6}f_{yyy} $

$(VII)\qquad f(x+b,y)\approx f + b f_x +\frac{b^2}{2}f_{xx} + \frac{b^3}{6}f_{xxx} $

$(VIII)\qquad f(x-c,y)\approx f - c f_x +\frac{c^2}{2}f_{xx} - \frac{c^3}{6}f_{xxx} $

$(IX)\qquad f(x,y)= f $

Let $a_1$ is the weight of equation (I), $a_2$ is the weight of equation (II) by equating $\sum a_i$*(equation number) =$0*f+0*f_x+...+ 1*f_{xy}+...+0*f_{xyy}$

Since we are having nine points we need nine equations to solve this but we are having more equations than unknown but only some combinations can give results. Choosing those combinations could be based on what order of accuracy required. Let fix our highest derivative term shouldn't be more than 3. If we tried to solve we can't obtain an exact solution for 9*9, the easiest way to get a solution is freeing some variables.

    clc
    clear all

    syms a1 a2 a3 a4 a5 a6 a7 a8 a7 a8 a9 a b c d % weight to each points
        eq1=a1 + a2 + a3 + a4 + a5 + a6 + a7 + a8+a9; % first order equation

        eq2= a1*b - a*a4 - a*a3 + a2*b + a7*b - a8*c;

        eq3=a1*d - a3*c - a6*c - a2*c + a4*d + a5*d;

        eq4=a^2*a3 + a^2*a4 + a1*b^2 + a2*b^2 + a7*b^2 + a8*c^2;

        eq5=a*a3*c - a2*b*c - a*a4*d + a1*b*d-1;

        eq6=a2*c^2 + a3*c^2 + a6*c^2 + a1*d^2 + a4*d^2 + a5*d^2;

        eq7=a1*b^3 - a^3*a4 - a^3*a3 + a2*b^3 + a7*b^3 - a8*c^3;

        eq8=a1*d^3 - a3*c^3 - a6*c^3 - a2*c^3 + a4*d^3 + a5*d^3;

        eq9=a^2*a4*d - a2*b^2*c - a^2*a3*c + a1*b^2*d;

        eq10=- a3*a^2*c - a4*a^2*d + a2*b*c^2 + a1*b*d^2;

        eq11 =d^2*b^2*a1+c^2*b^2*a2+a^2*c^2*a3+d^2*a^2*a4;

         sol1=solve(eq1,eq2,eq3,eq4,eq5,eq6,eq9,eq10,'a1','a2','a3','a4','a5','a6','a7','a8') % one of the possible solutions
    sol1=solve(eq1,eq2,eq3,eq4,eq5,eq8,eq9,eq10,'a1','a2','a3','a4','a5','a6','a7','a8') % another possible solution
    sol1=solve(eq1,eq2,eq3,eq4,eq5,eq7,eq9,eq10,'a1','a2','a3','a4','a5','a6','a7','a8') % another possible solution

    a9=1; % free variable
    w1=sol1.a1;
    w2=sol1.a2;
    w3=sol1.a3;
    w4=sol1.a4;
    w5=sol1.a5;
    w6=sol1.a6;
    w7=sol1.a7;
    w8=sol1.a8;
    w9=a9;

%     Test problem
    syms x y
    f=@(x,y) 1 +1*x +1*y +2*x*y +1*x^2 +1*y^2 +1*x^2*y+1*x*y^2+1*x^3+1*y^3+x^4*y;

f_x=diff(f,x);
f_xy=diff(f_x,y);

f_xy_00=subs(f_xy,[x y], [0 0]);

f_00=subs(f_xy,[x y],[0 0]); 
disp('exact solution is')
disp(f_00)
a=0.1;
b=0.1;
c=0.1;
d=0.1;
P00=f(0,0);
P10=f(b,0);
P11=f(b,d);
P01=f(0,d);
P_11=f(-a,d);
P_10=f(-a,0);
P_1_1=f(-a,-c);
P0_1=f(0,-c);
P1_1=f(b,-c);


f_xyn=w1*P11+w2*P1_1+w3*P_1_1+w4*P_11+w5*P01+w6*P0_1+w7*P10+w8*P_10+w9*P00; % numerical solution

disp('Numerical solution is')
disp(f_xyn) %sry I'm unable to use subs here so pls copy paste it agin in command window

Though all the answers are more or less same, they differ slighly based on what order we have considered. Similar to another answer, this sytem can be closed by omitting $f_{xxx}$, $f_{yyy}$ because they needs 4 points in $x$ or $y$ direction but we have only 3 points but we can calculate $f_{xxyy}$, it needs only 3 points in both the directions. If we include then the code become

clc
clear all

syms a1 a2 a3 a4 a5 a6 a7 a8 a7 a8 a9 a b c d % weight to each point
    eq1=a1 + a2 + a3 + a4 + a5 + a6 + a7 + a8+a9; % first order equation

    eq2= a1*b - a*a4 - a*a3 + a2*b + a7*b - a8*c;

    eq3=a1*d - a3*c - a6*c - a2*c + a4*d + a5*d;

    eq4=a^2*a3 + a^2*a4 + a1*b^2 + a2*b^2 + a7*b^2 + a8*c^2;

    eq5=a*a3*c - a2*b*c - a*a4*d + a1*b*d-1;

    eq6=a2*c^2 + a3*c^2 + a6*c^2 + a1*d^2 + a4*d^2 + a5*d^2;

    eq7=a1*b^3 - a^3*a4 - a^3*a3 + a2*b^3 + a7*b^3 - a8*c^3;

    eq8=a1*d^3 - a3*c^3 - a6*c^3 - a2*c^3 + a4*d^3 + a5*d^3;

    eq9=a^2*a4*d - a2*b^2*c - a^2*a3*c + a1*b^2*d;

    eq10=- a3*a^2*c - a4*a^2*d + a2*b*c^2 + a1*b*d^2;

    eq11 =d^2*b^2*a1+c^2*b^2*a2+a^2*c^2*a3+d^2*a^2*a4;

    sol1=solve(eq1,eq2,eq3,eq4,eq5,eq6,eq9,eq10,eq11,'a1','a2','a3','a4','a5','a6','a7','a8','a9');
    w1=sol1.a1;
    w2=sol1.a2;
    w3=sol1.a3;
    w4=sol1.a4;
    w5=sol1.a5;
    w6=sol1.a6;
    w7=sol1.a7;
    w8=sol1.a8;
 w9=sol1.a8;

%     Test problem
    syms x y
    f=@(x,y) 1 +1*x +1*y +2*x*y +1*x^2 +1*y^2 +1*x^2*y+1*x*y^2+1*x^3+1*y^3+x^4*y;

f_x=diff(f,x);
f_xy=diff(f_x,y);

f_xy_00=subs(f_xy,[x y], [0 0]);

f_00=subs(f_xy,[x y],[0 0]); 
disp('exact solution is')
disp(f_00)
a=0.1;
b=0.1;
c=0.1;
d=0.1;
P00=f(0,0);
P10=f(b,0);
P11=f(b,d);
P01=f(0,d);
P_11=f(-a,d);
P_10=f(-a,0);
P_1_1=f(-a,-c);
P0_1=f(0,-c);
P1_1=f(b,-c);
f_xyn=w1*P11+w2*P1_1+w3*P_1_1+w4*P_11+w5*P01+w6*P0_1+w7*P10+w8*P_10+w9*P00; % numerical solution

disp('Numerical solution is')
disp(f_xyn)  %sry I'm unable to use subs here so pls copy paste it again in the command window

Using polynomial fit

We can fit a 2-D polynomial over the domain and you can find the derivative value. First, we shall consider 2-D cubic polynomial then we shall find $f_{xy}$.

and matlab code is:

clc
clear all
close all
syms a0 a10 a01 a11 a20 a02  a12 a21 a30 a22 x y
syms a b c d
syms P00 P10 P11 P01 P_11 P_10 P_1_1 P0_1 P1_1
f=@(x,y) a0 +a10*x +a01*y +a11*x*y +a20*x^2 +a02*y^2 +a21*x^2*y+a12*x*y^2+a30*x^3;

f_x=diff(f,x);
f_xy=diff(f_x,y);

f_00=subs(f_xy,[x y],[0 0]);

p00=f(0,0);
p10=f(b,0);
p11=f(b,d);
p01=f(0,d);
p_11=f(-a,d);
p_10=f(-a,0);
p_1_1=f(-a,-c);
p0_1=f(0,-c);
p1_1=f(b,-c);

sol1=solve(p00-P00,p10-P10,p11-P11,p01-P01,p_11-P_11,p_10-P_10,p_1_1-P_1_1,p0_1-P0_1,'a0','a10','a01','a11','a20','a02','a12','a21');

F_xy=sol1.a11

$f_{xy} =\frac{(P_{10} - P_{11} - P_{-10} + P_{-11})}{(d*(a + b))}$ + $\frac{(P_{00} - P_{01} - P_{10} + P_{11})}{(b*d)} $- $\frac{(P_{00}*c^2-P_{01}*c^2-P_{-10}*c^2+P_{-11}*c^2-P_{00}*d^2+P_{0-1}*d^2+P_{-10}*d^2-P_{-1-1}*d^2)}{(a*c*d*(c + d))}$

The notation used here. $P_{xy}$ is the point located in the quadrent where $(x,y)$ =($0+x$, $0+y$) lies.

Similar to previous arguments, for $f_{xxyy}$ we can fit a quartic polynomial without $x^3$ and $y^3$ and the Matlab code is

clc
clear all
close all
syms a0 a10 a01 a11 a20 a02  a12 a21 a22 x y
syms a b c d
syms P00 P10 P11 P01 P_11 P_10 P_1_1 P0_1 P1_1
f=@(x,y) a0 +a10*x +a01*y +a11*x*y +a20*x^2 +a02*y^2 +a21*x^2*y+a12*x*y^2+a22*x^2*y^2;

f_x=diff(f,x);
f_xy=diff(f_x,y);

f_00=subs(f_xy,[x y],[0 0]);

p00=f(0,0);
p10=f(b,0);
p11=f(b,d);
p01=f(0,d);
p_11=f(-a,d);
p_10=f(-a,0);
p_1_1=f(-a,-c);
p0_1=f(0,-c);
p1_1=f(b,-c);

sol1=solve(p00-P00,p10-P10,p11-P11,p01-P01,p_11-P_11,p_10-P_10,p_1_1-P_1_1,p0_1-P0_1,p1_1-P1_1,'a0','a10','a01','a11','a20','a02','a12','a21','a22');

F_xy=sol1.a11 %f_xy result

$f_{xy} =\frac{(P_{00}*a^2*c^2 - P_{01}*a^2*c^2 - P_{10}*a^2*c^2 + P_{11}*a^2*c^2 - P_{00}*a^2*d^2 - P_{00}*b^2*c^2 + P_{01}*b^2*c^2 + P_{10}*a^2*d^2 + P_{0-1}*a^2*d^2 - P_{1-1}*a^2*d^2 + P_{-10}*b^2*c^2 - P_{-11}*b^2*c^2 + P_{00}*b^2*d^2 - P_{0-1}*b^2*d^2 - P_{-10}*b^2*d^2 + P_{-1-1}*b^2*d^2)}{(a*b*c*d*(a + b)*(c + d))}$

Test case:

clc
clear all
close all

syms x y
f=@(x,y) 1 +1*x +1*y +2*x*y +1*x^2 +1*y^2 +1*x^2*y+1*x*y^2+1*x^3+1*y^3+x^4*y;

f_x=diff(f,x);
f_xy=diff(f_x,y);

f_xy_00=subs(f_xy,[x y], [0 0]);

f_00=subs(f_xy,[x y],[0 0]);
a=0.1;
b=0.1;
c=0.1;
d=0.1;
P00=f(0,0);
P10=f(b,0);
P11=f(b,d);
P01=f(0,d);
P_11=f(-a,d);
P_10=f(-a,0);
P_1_1=f(-a,-c);
P0_1=f(0,-c);
P1_1=f(b,-c);

disp('exact solution is')
disp(f_00)
f_22=(P00*a^2*c^2 - P01*a^2*c^2 - P10*a^2*c^2 + P11*a^2*c^2 - P00*a^2*d^2 - P00*b^2*c^2 + P01*b^2*c^2 + P10*a^2*d^2 + P0_1*a^2*d^2 - P1_1*a^2*d^2 + P_10*b^2*c^2 - P_11*b^2*c^2 + P00*b^2*d^2 - P0_1*b^2*d^2 - P_10*b^2*d^2 + P_1_1*b^2*d^2)/(a*b*d*(a + b)*(c^2 + d*c));


disp('Numerical solution is')
disp(f_22)

Though there are a lot of ways to derive it, I personally prefer FD derived using polynomial because of its simplicity and accuracy of last $f_{xy}$ is higher than the previous one because it satisfies more terms in Taylors series.

Answer 3

In your sketch, you are having 9 grid points so you could have fit all 9 values to a 2-D cubic polynomial. Then the Taylor series expansion becomes

$(I)\qquad f(x+b,y+d)\approx f + b f_x+d f_y +\frac{b^2}{2}f_{xx} +bdf_{xy} +\frac{d^2}{2}f_{yy} + \frac{b^3}{6}f_{xxx} + \frac{d^3}{6}f_{yyy} + \frac{1}{2} b^2df_{xxy}+ \frac{1}{2} d^2bf_{xyy}$ $(II)\qquad f(x+b,y-c)\approx f + b f_x-c f_y +\frac{b^2}{2}f_{xx} -bcf_{xy} +\frac{c^2}{2}f_{yy}+ \frac{b^3}{6}f_{xxx} - \frac{c^3}{6}f_{yyy} - \frac{1}{2} b^2cf_{xxy}+ \frac{1}{2} c^2bf_{xyy}$ $(III)\qquad f(x-a,y-c)\approx f - a f_x-c f_y +\frac{a^2}{2}f_{xx} +acf_{xy} +\frac{c^2}{2}f_{yy}- \frac{a^3}{6}f_{xxx} - \frac{c^3}{6}f_{yyy} - \frac{1}{2} a^2cf_{xxy}- \frac{1}{2} a^2cf_{xyy}$ $(IV)\qquad f(x-a,y+d)\approx f - a f_x+d f_y +\frac{a^2}{2}f_{xx} -adf_{xy} +\frac{d^2}{2}f_{yy}- \frac{a^3}{6}f_{xxx} + \frac{d^3}{6}f_{yyy} + \frac{1}{2} a^2df_{xxy}- \frac{1}{2} a^2df_{xyy}$

$(V)\qquad f(x,y+d)\approx f +d f_y +\frac{d^2}{2}f_{yy} + \frac{d^3}{6}f_{yyy} $

$(VI)\qquad f(x,y-c)\approx f -c f_y +\frac{c^2}{2}f_{yy} - \frac{c^3}{6}f_{yyy} $

$(VII)\qquad f(x+b,y)\approx f + b f_x +\frac{b^2}{2}f_{xx} + \frac{b^3}{6}f_{xxx} $

$(VIII)\qquad f(x-c,y)\approx f - c f_x +\frac{c^2}{2}f_{xx} - \frac{c^3}{6}f_{xxx} $

$(IX)\qquad f(x,y)= f $

Let $a_1$ be the weight of equation (I), $a_2$be the weight of equation (II) by equating $\sum a_i\cdot$ (equation number) =$0\cdot f+0\cdot f_x+\ldots+ 1\cdot f_{xy}+\ldots+0\cdot f_{xyy}$.

You can obtain a system of 9 linear equations with 9 unknowns, and by solving them you can obtain $a_i$, Then you can obtain $f_{xy}$. You may use a symbolic tool to solve that in Matlab, Mathematica, Maple, python etc.

I think this system ends up in the singular case for $f_{xy}$ calculation using 9 points. In addition to that, we have 10 equations with 9 variables so satisfying all terms of Taylor's series up to the third order term is impossible for this system. The easiest way to make it deterministic is freeing some variable and compromising higher-order terms so we can get a lot of solutions to this problem. Matlab script used is:

clear all; clc    
syms a1 a2 a3 a4 a5 a6 a7 a8 a7 a8 a9 a b c d % weight to each points
    eq1=a1 + a2 + a3 + a4 + a5 + a6 + a7 + a8+a9; % first order equation

    eq2= a1*b - a*a4 - a*a3 + a2*b + a7*b - a8*c;

    eq3=a1*d - a3*c - a6*c - a2*c + a4*d + a5*d;

    eq4=a^2*a3 + a^2*a4 + a1*b^2 + a2*b^2 + a7*b^2 + a8*c^2;

    eq5=a*a3*c - a2*b*c - a*a4*d + a1*b*d;

    eq6=a2*c^2 + a3*c^2 + a6*c^2 + a1*d^2 + a4*d^2 + a5*d^2;

    eq7=a1*b^3 - a^3*a4 - a^3*a3 + a2*b^3 + a7*b^3 - a8*c^3;

    eq8=a1*d^3 - a3*c^3 - a6*c^3 - a2*c^3 + a4*d^3 + a5*d^3;

    eq9=a^2*a4*d - a2*b^2*c - a^2*a3*c + a1*b^2*d;

    eq10=- a3*a^2*c - a4*a^2*d + a2*b*c^2 + a1*b*d^2;

    sol1=solve(eq1,eq2,eq3,eq4,eq5,eq6,eq7,eq9,'a1','a2','a3','a4','a5','a6','a7','a8') % one of the possible solutions

For different equation combinations, you may get different solutions, make sure you are not trading lower-order terms to make it deterministic.

You can then find the errors in your formulas by applying them to the Taylor expansion of an arbitrary function. They will have the form$$G(a,b,c,d)\frac{\partial^{h+k}f}{\partial x^h\partial y^k}$$ The terms of the lowest order are called the "leading error terms" and are usually the most important. They are called the truncation error because they are caused by taking only a finite number of terms in the Taylor series. Of course, to use more terms you would need more data points. The most accurate formulas are the ones with the smallest values of $G(a,b,c,d)$. This is what you might hope to achieve by employing more of the data.

Something to be aware of when handling irregular grids is that the errors you will obtain this way depend on the point around which you expand the solution. In other words, the accuracy of a finite-difference expression is tied to a particular location. When you analyse the accuracy of a finite-difference method that seeks an equilibrium among many terms, then every term must be evaluated at the same place.

Answer 4

The answer from @Philip-Roe on Aug 2 '17 at 1:34 is the correct one. @AGN proposal of using a cubic term in $x$ but not in $y$ is more than awkward.

A less rigorous derivation starts from the uniform case. Many textbooks (for example Abramovitz and Stegun) give for a uniform discretization

$$\frac{\partial f}{\partial u \partial v}(u,v) \approx \frac{f(u+m,v+m)-f(u+m,v-m)-f(u-m,v+m)+f(u-m,v-m)}{4m^2}$$ to second order.

We apply a variable transformation $x(u)$ and $y(v)$

$$\frac{\partial^2 f}{\partial x \partial y}(x,y) = \left(\frac{\partial x}{\partial u}\right)^{-1}\frac{\partial }{\partial u}\left(\left(\frac{\partial y}{\partial v}\right)^{-1}\frac{\partial f}{\partial v}\right)(u,v) = \left(\frac{\partial x}{\partial u} \frac{\partial y}{\partial v} \right)^{-1} \frac{\partial^2 f}{\partial u \partial v}(x(u),y(v))$$.

If we now approximate the Jacobians by $\frac{\partial x}{\partial u} \approx \frac{b+a}{2m}$, $\frac{\partial y}{\partial v} \approx \frac{d+c}{2m}$, which is also second order, we obtain the formula of @benno and @Philip-Roe.

Note that we could also use the non-uniform 3 points formula for the Jacobian. This is where @Philip-Roe derivation is more interesting as it is clearly optimal for the given explicit biquadratic parameterization that anybody would relate to naturally.