In the 4D Henon-Heiles system, it is well-known for certain parameters the attractor is a 2D torus. I am wondering how can we plot this actual torus (embedded in 3D) by somehow projecting all 4 components to some 3D space and to observe if a torus-shaped object will pop out.
I have seen people visualize this 2D torus simply by choosing 2 or 3 out of the 4 variables and plot. An example of the former is here (look for the case of quasi-periodic). An example of the latter is:
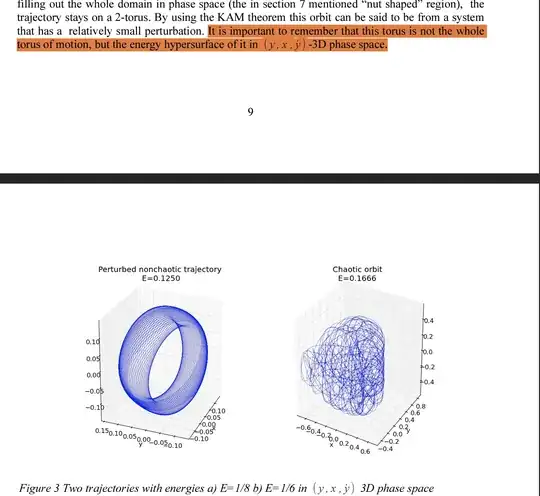
where the author said (in highlighted text) that the visualized torus is not the "whole torus of motion" as it is plotted using only 3 out of 4 variables of the system.
I have also seen machine-learning oriented "nonlinear dimensionality reduction" or "manifold learning" methods such as ISOMAP. However, I do not think these are the relevant methods because they depend on choosing certain parameters such as number of neighbors to consider and some of them are even stochastic so changes every time you use them, whereas the 2D torus I am after is a fundamental and concrete property of the system and its recovery shouldn't be stochastic or depend on some choice of parameters...
This seems to be a straight-forward thing to do, but so far I have been stuck on even finding an example where the complete Henon-Heiles 2D torus is visualized (this must involve somehow projecting to a 3D space using all 4 variables).