I need to solve the following system of differential equations.
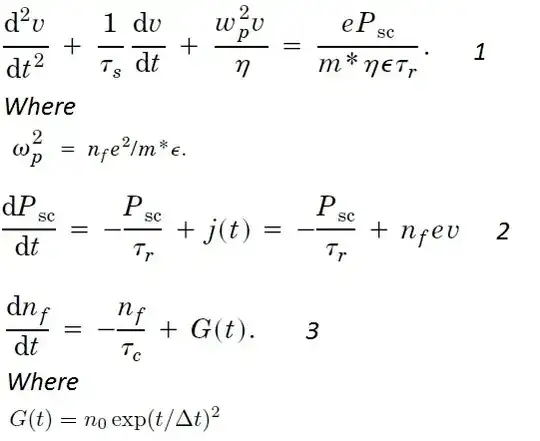
When I have the solutions for $n_f$ and $v$, I need to find and plot $J=-e_\cdot n_{f} \cdot v$.
I wrote a code in matlab with all ODEs like this:
function systemSolve
clc
tr=50e-12; % Recombination lifetime
n0=1e11; % Density of free carriers (Recordar que es 1e17 cm-3)
tc=2e-12; % Trapping time
ts=30e-15; % Carrier scattering time
m=0.067*9.11e-31; % effective mass GaAs
ev=8.854e-12; % permitivity
n=900; % factor geometry
q=1.6e-19 % electron charge
de=50e-15 % delta t
timeRange=[0 0.1e-12];
initialConditionVector=[0;1e-15;1e-15;1e-15];
[t,x]=ode45(@xprime,timeRange,initialConditionVector);
figure(1),plot(t,x(:,1))
J=q*x(:,3).*x(:,1);
figure(2),plot(t,J)
function f=xprime(t,x)
f=[x(4); ...
-(x(2)/tr)+(x(3)*q*x(1)); ...
-(x(3)/tc)+(n0*(exp((t/de)^2))); ...
-((1/ts)*x(4))-(((x(3)*q^2)/m*ev)*x(1)/n)+(q*x(2)/(m*n*ev*tr))];
end
end
I suppose that:
$x_1=v$
$x_2=P_{sc}$
$x_3=n_f$
$x_4=x'_1$
I expect to find a current pulse like figure 1 but I get a exponential solution.

What is wrong in this code and can you suggest me how i can solve this problem?