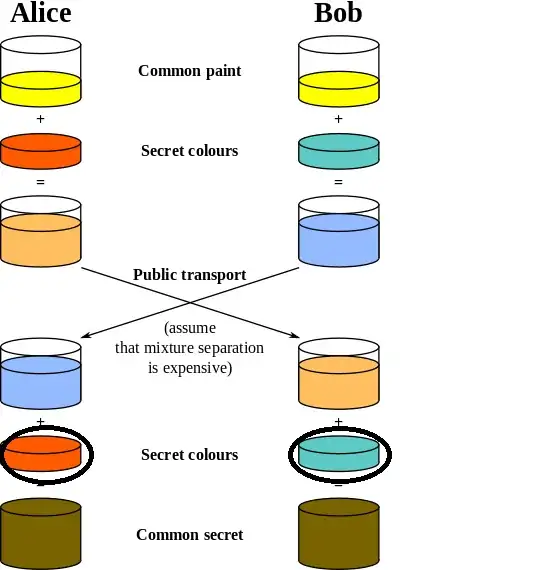
I understand the diagram up till the point where Bob and Alice do a "Public transport" of their respective mixture. I am wondering how do Bob and Alice know what secret colour to add ( circled picture ) to get the Common secret

I understand the diagram up till the point where Bob and Alice do a "Public transport" of their respective mixture. I am wondering how do Bob and Alice know what secret colour to add ( circled picture ) to get the Common secret
The best way to understand the realms of Diffie–Hellman key exchange is to throw a glance on the mathematical procedures ut follows and which I am going to explain:


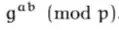
But where is the answer to your question ? It is highlighted by the second step of the algorithm: it means Bob & Alice have not to know how to choose the circled pictures but they choose them randomly.
I think the diagram explains it quite well, but I'll give a step-by-step explanation:
This is a really nice parallel to how the maths works:
If you just want to understand the concept and not the math, which is fine, I would like to give you a semi-mathematical explanation, but in fact your model with the colors is rly confusing for me:
Imagine Alice and Bob agree on any number random number g. Lets say g = 5. Now each of them choses a secret number. Alices chooses a = 2 and Bob chooses b = 3. The public numbers are calculated by A = g^a = 5^2 = 25 for Alice and B = g^b = 5^3 = 125 for Bob. Now, as Alice knows B = 125 and Bob knows A = 25, as those are the public numbers. They both pow this number by their private numbers and Alice gets B^a = 125^2 = 15625 and Bob gets A^b = 25^3 = 15625. So 15625 is the shared number.
In fact we need some more restrictions to have a save exchange, wikipedia offers a good explanation, as begueradj does.