3

I would like to plot the surface 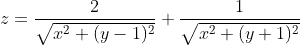over 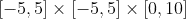. I cannot figure out how to show the two "holes" of the surface that result due to its intersection with the plane.

I tried the following but I cannot get the holes to be smooth given the limited samples that I am only afforded.

\documentclass[border=2pt]{standalone}
\usepackage{pgfplots}
\usepgfplotslibrary{patchplots}
\pgfplotsset{compat=1.9}
\begin{document}
\begin{tikzpicture}
\begin{axis}[
axis lines=center,
width=15cm,
view={120}{45},
enlargelimits=false,
grid=major,
xlabel=$x$,
ylabel=$y$,
zlabel=$\varphi$, xmin=-5,xmax=5, ymin=-5,ymax=5, zmin=-1,zmax=10
]
\addplot3[] (0,0,0);
\def\ra{0.58}\def\ga{0.26}\def\ba{0.64}
\def\rb{0.91}\def\gb{0.85}\def\bb{0.92}
\addplot3[patch, patch type=bilinear,
mesh/color input=explicit mathparse, samples=66,
z buffer=sort,
domain=-1:1,
y domain=-2:2, restrict z to domain=0:10,
opacity=0.8,
point meta={symbolic={\rb+(10-z)/10*(\ra-\rb),
\gb+(10-z)/10*(\ga-\gb),
\bb+(10-z)/10*(\ba-\bb)}},]
({x}, {y}, {2/sqrt((x*x) + ((y-1)*(y-1))) + 1/sqrt((x*x) + ((y+1)*(y+1)))});
\end{axis}
\end{tikzpicture}
\end{document}

I also tried parametrizing around the holes but I do not know how to complete the rest of the graph. Please advise. Thank you.

\documentclass[border=2pt]{standalone}
\usepackage{pgfplots}
\usepgfplotslibrary{patchplots}
\pgfplotsset{compat=1.9}

\begin{document}
\begin{tikzpicture}
\begin{axis}[
axis lines=center,
width=15cm,
view={120}{45},
enlargelimits=false,
grid=major,
samples=20, 
xlabel=$x$,
ylabel=$y$,
zlabel=$\varphi$, xmin=-5,xmax=5, ymin=-5,ymax=5, zmin=0,zmax=10
]


\addplot3[] (0,0,0);


\def\ra{0.58}\def\ga{0.26}\def\ba{0.64}
\def\rb{0.91}\def\gb{0.85}\def\bb{0.92}


\addplot3[patch,patch type=bilinear,
mesh/color input=explicit mathparse,
z buffer=sort, samples = 40,
domain=0.1:1,
y domain=0:2pi,
opacity=0.6,
point meta={symbolic={\rb+((10-z)/10)(\ra-\rb),
\gb+((10-z)/10)(\ga-\gb),
\bb+((10-z)/10)(\ba-\bb)}}]
({xcos(deg(y))}, {-1+xsin(deg(y))}, {min(2/sqrt(xx - (4xsin(deg(y))) + 4) + 1/sqrt(xx), 10)});


\addplot3[patch,patch type=bilinear,
mesh/color input=explicit mathparse,
z buffer=sort,samples=40,
domain=0.2:1,
y domain=0:2pi,
opacity=0.6,
point meta={symbolic={\rb+((10-z)/10)(\ra-\rb),
\gb+((10-z)/10)(\ga-\gb),
\bb+((10-z)/10)(\ba-\bb)}}]
({xcos(deg(y))}, {1+xsin(deg(y))}, {min(2/sqrt(xx) + 1/sqrt(xx + (4xsin(deg(y))) + 4), 10)});


\end{axis}
\end{tikzpicture}
\end{document}
Allan Ray
  • 83

1 Answers1

2

Just for fun.

Compile with Asymptote.

Run in cmd: asy -f pdf -render=4 xcvxc.asy (for pdf)

Run in cmd: asy -noprc -f pdf -V -render=4 xcvxc.asy (for interaction)

// name: xcvxc.asy

import graph3;
import smoothcontour3;
import contour3;
import palette;


size(12cm,IgnoreAspect);
currentprojection=orthographic(1,-2,1);


real f(real x, real y, real z) {return 2/(sqrt(x^2+(y-1)^2))+1/(sqrt(x^2+(y+1)^2))-z;}


// Code 1 (recommended)
surface s=implicitsurface(f,(-1,-2,0),(2,2,6),overlapedges=true);
s.colors(palette(s.map(zpart),Rainbow()));
draw(s,render(merge=true));


/*
// Code 2
surface s=surface(contour3(f,(-1,-2,0),(2,2,5),25)); 
// > 30, for my computer, error: out of memory
s.colors(palette(s.map(zpart),Rainbow()));
draw(s,render(compression=Low,merge=true));
*/


xaxis3("$x$",Bounds,InTicks);
yaxis3("$y$",Bounds,InTicks(beginlabel=false));
zaxis3("$z$",Bounds,InTicks);

Code 1:

enter image description here

Code 2:

enter image description here

For more information, see smoothcontour3. or have look at here.