The equation, I am using is going outside the margin in Springer LNCS format. The MWE is shown below.
\documentclass[runningheads]{llncs}
\usepackage{amsmath,amssymb}
\usepackage{mathtools, nccmath}
\begin{document}
\begin{align}
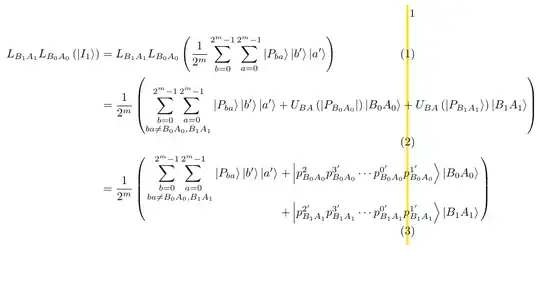
L_{B_{1} A_{1}} L_{B_{0} A_{0}}\left(\left|I_{1}\right\rangle\right) & =L_{B_{1} A_{1}} L_{B_{0} A_{0}}\left(\frac{1}{2^{m}} \sum_{b=0}^{2^{m}-1} \sum_{a=0}^{2^{m}-1}\left|P_{b a}\right\rangle\left|b^{\prime}\right\rangle\left|a^{\prime}\right\rangle\right)\\
& =\frac{1}{2^{m}}\left(\underset{b a \neq B_{0} A_{0}, B_{1} A_{1}}{\displaystyle\sum_{b=0}^{2^{m}-1} \sum_{a=0}^{2^{m}-1}}\left|P_{ba}\right\rangle\left|b^{\prime}\right\rangle\left|a^{\prime}\right\rangle+U_{B A}\left(\left|P_{B_{0} A_{0}}\right|\right)\left|B_{0} A_{0}\right\rangle+U_{B A}\left(\left|P_{B_{1} A_{1}}\right\rangle\right)\left|B_{1} A_{1}\right\rangle\right) \\
& =\frac{1}{2^{m}}
\left(\begin{array}{rl}
\underset{b a \neq B_{0} A_{0}, B_{1} A_{1}}{\displaystyle\sum_{b=0}^{2^{m}-1} \sum_{a=0}^{2^{m}-1}}\left|P_{b a}\right\rangle\left|b^{\prime}\right\rangle\left|a^{\prime}\right\rangle &+\left|p_{B_{0} A_{0}}^{2} p_{B_{0} A_{0}}^{3^{\prime}} \cdots p_{B_{0} A_{0}}^{0^{\prime}} p_{B_{0} A_{0}}^{1^{\prime}}\right\rangle\left|B_{0} A_{0}\right\rangle \\
&+\left|p_{B_{1} A_{1}}^{2^{\prime}} p_{B_{1} A_{1}}^{3^{\prime}} \cdots p_{B_{1} A_{1}}^{0^{\prime}} p_{B_{1} A_{1}}^{1^{\prime}}\right\rangle\left|B_{1} A_{1}\right\rangle
\end{array}\right)
\end{align}
\end{document}
Let the imaginary yellow line is the boarder. You can see that the equation crosses this margin. Whenever I am trying, it is showing errors. Somebody please help me to correct it.
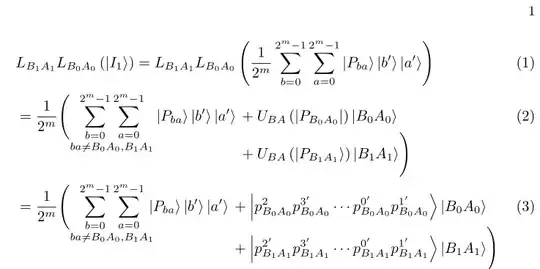
2^{\prime}as2'produces identical output. – David Carlisle Sep 03 '21 at 07:42