I want to align equations inside an enumerate environment or to get a similar result using another environment. Here's the actual code:
\documentclass{article}
\usepackage{amsthm}
\begin{document}
\begin{enumerate}
\item $\forall a,b \in K \qquad a + b \in K$
\item $\forall a,b \in K \qquad a \cdot b \in K$
\item $\forall a,b \in K \qquad a + b = b + a$
\item $\forall a,b,c \in K \qquad a + (b + c) = (a + b) + c$
\item $\exists n_{+} \in K \ \forall a \in K \qquad a + n_{+} = a$
\item $\forall a \in K \ \exists a_{+}' \in K \qquad a + a_{+}' = n_{+}$
\item $\forall a,b \in K \qquad a \cdot b = b \cdot a$
\item $\forall a,b,c \in K \qquad a \cdot (b \cdot c) = (a \cdot b) \cdot c$
\item $\forall a,b,c \in K \qquad a \cdot (b + c) = a \cdot b + a \cdot c$
\item $\exists n_{\cdot} \in K \ \forall a \in K\backslash\{n_{+}\} \qquad a \cdot n_{\cdot} = a$
\item $\forall a \in K\backslash\{n_{+}\} \ \exists a_{\cdot}' \in K \qquad a \cdot a_{\cdot}' = n_{\cdot}$
\end{enumerate}
\end{document}
I want the equations in the second column would be left aligned.
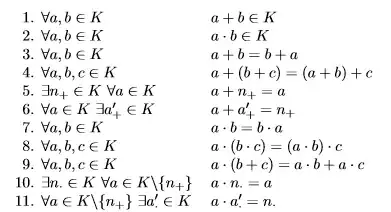
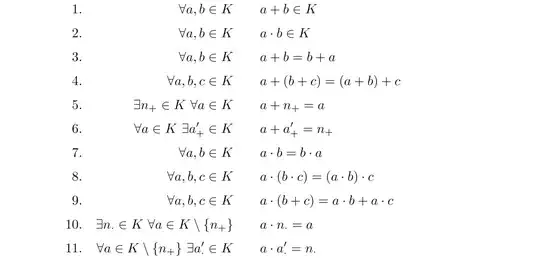
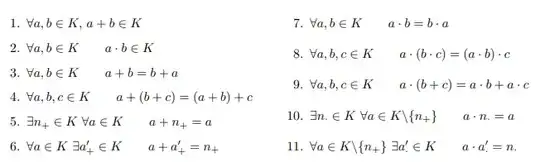
\setminus, not\backslash, in the final two rows. – Mico Sep 18 '21 at 20:29