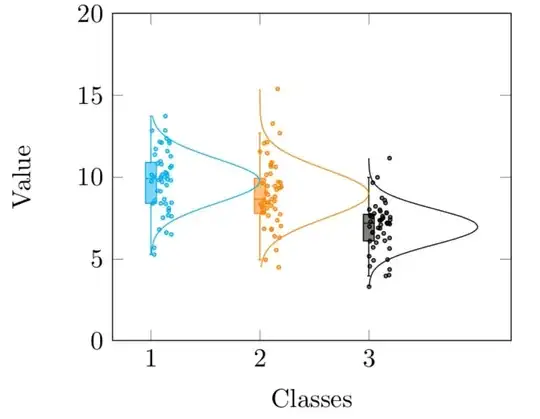
After looking at some plots on OriginLab which combine boxplots with the distribution curve and the raw data, I wanted to do something similar in PGFPlots. I found some interesting work already here. Building on this, I created the following plot. I see that the presentation of the plot and some visuals can be improved. The issue here is the distribution curves are too big. Would it be possible to do compress them? To plot these curves, I manually inserted the domain values along with the mean and variance of the respective datasets. Please find the code of the plots below:
\documentclass[border=5mm]{standalone}
\usepackage{pgfplots}
\usepackage{pgfplotstable}
\usepackage{tikz}
\usepgfplotslibrary{statistics}
\definecolor{saffron}{HTML}{FF9933}
\definecolor{brickred}{HTML}{F96302}
\definecolor{grenadier}{HTML}{D44700}
\definecolor{grandisorange}{HTML}{FFCF79}
\pgfplotsset{
jitter/.style={
x filter/.code={\pgfmathparse{\pgfmathresult+rnd*#1}}
},
jitter/.default=0.1
}
\begin{document}
\begin{tikzpicture}
%--- PLOTTING DATA ---%
\pgfplotstableread[row sep = \]{
x data \
1 13.7219 \
1 10.1599 \
1 10.7791 \
1 9.5097 \
1 6.6125 \
1 9.9981 \
1 8.1011 \
1 11.2725 \
1 10.105 \
1 12.0993 \
1 10.5794 \
1 11.7101 \
1 9.9047 \
1 9.8042 \
1 7.6605 \
1 8.3959 \
1 10.2814 \
1 5.2662 \
1 9.861 \
1 10.2249 \
1 9.8222 \
1 12.3537 \
1 8.3699 \
1 10.6791 \
1 9.9997 \
1 10.1496 \
1 10.833 \
1 12.2066 \
1 6.4986 \
1 10.0193 \
1 9.1327 \
1 8.4368 \
1 9.162 \
1 7.5179 \
1 6.7939 \
1 7.9497 \
1 12.8426 \
1 5.68 \
1 12.1573 \
1 8.3866 \
1 12.8471 \
1 7.6095 \
1 8.569 \
1 9.6969 \
1 10.9593 \
1 11.5845 \
1 9.7342 \
1 11.3692 \
1 12.067 \
1 8.6466 \
}\dataA
\pgfplotstableread[row sep = \]{
x data \
2 10.6485 \
2 12.1327 \
2 8.3516 \
2 6.8364 \
2 9.087 \
2 9.7096 \
2 11.559 \
2 12.0554 \
2 8.6433 \
2 12.6913 \
2 9.6378 \
2 7.6447 \
2 8.1357 \
2 8.5953 \
2 6.7866 \
2 4.49 \
2 6.3017 \
2 15.3823 \
2 7.0121 \
2 13.2661 \
2 10.2045 \
2 8.5268 \
2 8.4672 \
2 8.8128 \
2 9.659 \
2 7.7304 \
2 10.6145 \
2 8.4329 \
2 10.7728 \
2 9.4515 \
2 8.1012 \
2 9.4598 \
2 8.2576 \
2 9.2268 \
2 6.8337 \
2 7.8323 \
2 10.8946 \
2 10.1366 \
2 6.3889 \
2 5.5418 \
2 9.3919 \
2 9.3976 \
2 7.3574 \
2 11.4605 \
2 7.8299 \
2 8.0555 \
2 9.3363 \
2 8.2947 \
2 8.9302 \
2 4.9484 \
}\dataB
\pgfplotstableread[row sep = \] {
x data \
3 11.1575 \
3 6.3445 \
3 7.6768 \
3 6.8726 \
3 6.1151 \
3 8.0012 \
3 7.3762 \
3 7.2804 \
3 4.5495 \
3 8.7247 \
3 7.1302 \
3 5.6378 \
3 9.6559 \
3 7.6132 \
3 7.7771 \
3 7.182 \
3 5.9942 \
3 7.8322 \
3 3.3087 \
3 7.5138 \
3 9.9824 \
3 7.4416 \
3 7.5475 \
3 8.0151 \
3 7.9198 \
3 6.2829 \
3 7.3886 \
3 4.9581 \
3 4.36 \
3 6.6295 \
3 7.805 \
3 6.5626 \
3 7.0912 \
3 7.6083 \
3 6.0897 \
3 8.5777 \
3 4.0153 \
3 8.4225 \
3 7.2019 \
3 5.1663 \
3 3.9603 \
3 7.5764 \
3 7.3596 \
3 8.2149 \
3 6.9772 \
3 4.9117 \
3 6.6025 \
3 6.8943 \
3 7.1555 \
3 5.7075 \
}\dataC
\begin{axis}
[boxplot/draw direction=y,
xlabel={Classes},
ylabel={Value},
height=6cm,
ymin=0,ymax=20,
xtick={1, 2, 3},
boxplot/box extend=0.1,
boxplot/whisker extend=0.03,
every axis plot/.append style={fill,fill opacity=0.5},
cycle list={{cyan},{orange},{black}}]
\addplot+ [boxplot] table [y index = 1] {\dataA};
\addplot+ [boxplot] table [y index = 1] {\dataB};
\addplot+ [boxplot] table [y index = 1] {\dataC};
\addplot+ [jitter=0.2, only marks, mark size=.7pt, xshift = 0mm] table [y index = 1] {\dataA};
\addplot+ [jitter=0.2, only marks, mark size=.7pt, xshift = 0mm] table [y index = 1] {\dataB};
\addplot+ [jitter=0.2, only marks, mark size=.7pt, xshift = 0mm] table [y index = 1] {\dataC};
\addplot+ [domain=5.266:13.7219, fill=none, smooth] ({1+1exp(-pow(x-9.76243,2)/3.6622)},x);
\addplot+ [domain=4.489:15.3822, fill=none, smooth] ({2+1exp(-pow(x-8.98630,2)/4.4150)},x);
\addplot+ [domain=3.309:11.1574, fill=none, smooth] ({3+1*exp(-pow(x-6.96339,2)/2.3290)},x);
\end{axis}
\end{tikzpicture}
\end{document}
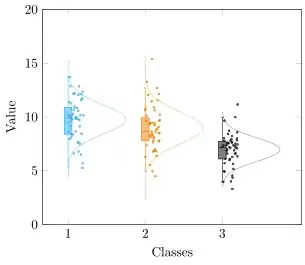
1+0.7*exp(...– dexteritas Sep 24 '21 at 12:00