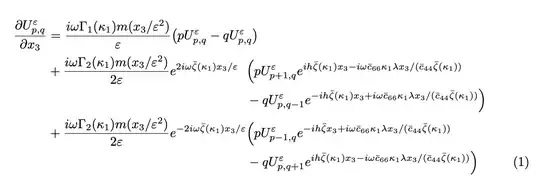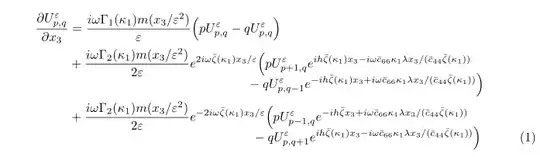I am having trouble aligning the second block in my example below...
\documentclass{article}
\usepackage{amsmath}
\usepackage{amssymb}
\begin{document}
\begin{alignat}{2}\nonumber
\frac{\partial U^\varepsilon_{p,q}}{\partial x_3} &= \frac{i\omega\Gamma_1(\kappa_1) m(x_3/\varepsilon^2)}{\varepsilon}\bigg(pU^\varepsilon_{p,q} - qU^\varepsilon_{p,q}\bigg) \ \nonumber
&+\frac{i\omega\Gamma_2(\kappa_1) m(x_3/\varepsilon^2)}{2\varepsilon}e^{2i\omega\bar\zeta(\kappa_1)x_3/\varepsilon}&&\bigg(pU^\varepsilon_{p+1,q}e^{ih\bar\zeta(\kappa_1)x_3 - i\omega\bar{c}{66}\kappa_1\lambda x_3/(\bar{c}{44}\bar{\zeta}(\kappa_1))} \ \nonumber
&\phantom{+} &&-qU^\varepsilon_{p,q-1}e^{-ih\bar\zeta(\kappa_1)x_3 + i\omega\bar{c}{66}\kappa_1\lambda x_3/(\bar{c}{44}\bar{\zeta}(\kappa_1))}\bigg) \ \nonumber
&+\frac{i\omega\Gamma_2(\kappa_1) m(x_3/\varepsilon^2)}{2\varepsilon}e^{-2i\omega\bar\zeta(\kappa_1)x_3/\varepsilon}&&\bigg(pU^\varepsilon_{p-1,q}e^{-ih\bar{\zeta}x_3 + i\omega\bar{c}{66}\kappa_1\lambda x_3/(\bar{c}{44}\bar{\zeta}(\kappa_1))} \
&\phantom{+} &&-qU^\varepsilon_{p,q+1}e^{ih\bar{\zeta}(\kappa_1)x_3 - i\omega\bar{c}{66}\kappa_1\lambda x_3/(\bar{c}{44}\bar{\zeta}(\kappa_1))}\bigg)
\end{alignat}
\end{document}
The second line where \bigg(p appears should not have a large space between there and the exponential previous to it, could someone lend me a piece of advice please? Thanks.